函数、判断与迭代

字数统计: 4.4k字   |   阅读时长: 20分

1 函数

只要一段代码需要复制粘贴的次数超过两次，就应该考虑编写一个函数。
创建一个新函数，需要以下3个关键步骤：
1）为函数选择一个名称。两种命名法：下划线法“snake_case”或首字母大写法“camelCase”。
2）列举出function中所用的输入，即参数。
3）将已经编写好的代码放在函数体中。

条件过滤器：stopifnot()，该函数防止无关的输入参数进入到函数中运算。
省略符号：函数的参数中加入特殊的省略符号表示可能需要传递给其他函数的参数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
> sdFunc <- function(x, type = 'sample', ...) {
+     stopifnot(is.numeric(x),
+               length(x) > 0,
+               type %in% c('sample', 'population'))
+     x <- x[!is.na(x)]
+     n <- length(x)
+     m <- mean(x, ...)
+     if (type == 'sample') {
+         sd <- sqrt(sum((x - m) ^ 2) / (n - 1))
+     }
+     if (type == 'population') {
+         sd <- sqrt(sum((x - m) ^ 2) / (n))
+     }
+     return(sd)
+ }
> y <- c(1:10, 50)
> sdFunc(y, type = 'sample', trim = 0.1)
[1] 14.21619

匿名函数：也就是没有名字的函数，通常在向量化计算中遇到。
二元运算符：四则运算符号称为二元运算符，这种运算符也是一种函数。二元运算符也可以自定义，需要加上引号，并且使用百分号以方便区分。一般只能输入两个变量，如果输入多个变量，可以使用Reduce()函数将二元运算符进行简化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#匿名函数进行向量化计算
> set.seed(1)
> m <- matrix(rnorm(100), 10, 10)
> apply(m, 1, function(x) max(x) - min(x))
 [1] 3.028072 1.917814 2.013716 3.809981 2.963893 2.800868 2.868058 2.936307
 [9] 2.324638 2.762133
#二元运算符
> (Prod <- 1:4 * 4:1)
> (Prod <- '*'(1:4, 4:1))
[1] 4 6 6 4
#自定义二元运算符，找出两个集合的交集
> a <- c('apple', 'banana', 'orange')
> b <- c('grape', 'banana', 'orange')
> '%it%' <- function(x, y) {
+     intersect(x, y)
+ }
> a %it% b
[1] "banana" "orange"
> c <- c('grape', 'banana', 'other')
> a %it% b %it% c
[1] "banana"
> L <- list(a, b, c)
> Reduce('%it%', L)
[1] "banana"

2 判断

简单条件判断：if
多重条件判断：if-else
向量化条件判断：ifelse()，第一个参数是逻辑判断，如果为真则返回yes参数对应的值，为假则返回no参数对应的值。该函数本身可以嵌套在自身的参数中，进行多重分支的条件判断。
多重分支条件判断：switch()，第一个参数负责判断，参数如果是数值，则取后面相应位置的参数；如果为字符串，则与后面的参数精确匹配，返回相应数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
> num <- 5
> if (num %% 2) cat(num, 'is odd')
5 is odd
#if-else
> num <- 10
> if (num %%3 == 1) {
+     cat('mode is', 1)
+ } else if (num %% 3 == 2){
+     cat('mode is', 2)
+ } else {
+     cat('mode is', 0)
+ }
mode is 1
#ifelse()
> num <- 1:6
> ifelse(num %% 2 == 0, yes = 'even', no = 'odd')
[1] "odd"  "even" "odd"  "even" "odd"  "even"
> set.seed(1)
> num <- sample(20:70, 20, replace = TRUE)
> res <- ifelse(num >50, '老年', ifelse(num < 30, '青年', '中年'))
> res
 [1] "青年" "老年" "青年" "老年" "中年" "老年" "中年" "中年" "老年" "老年"
[11] "中年" "中年" "老年" "老年" "青年" "青年" "青年" "中年" "中年" "老年"
#switch
> switch(2, 'banana', 'apple', 'other')
[1] "apple"
> price <- function(fruit){
+     switch(fruit, apple = 10, orange = 12, grape = 16, banana = 8, 0)
+ }
> price('apple')
[1] 10

3 迭代

有两种重要的迭代方式：命令式编程和函数式编程，其中，命令式编程包括for循环和while循环，而函数式编程可以将重复代码提取出来，使每个普通的for循环都可以通过函数来完成。

3.1 命令式编程

3.1.1 for 循环

假设有一个简单的tibble，需要计算每列的中位数，用for循环可以减少重复工作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
> library(tidyverse)
> df <- tibble(
+     a = rnorm(10),
+     b = rnorm(10),
+     c = rnorm(10),
+     d = rnorm(10)
+ )
> df
# A tibble: 10 x 4
         a       b      c      d
     <dbl>   <dbl>  <dbl>  <dbl>
 1  0.400  -0.842   0.860 -0.334
 2 -0.0210  0.175  -0.774  0.397
 3 -1.16   -0.893  -1.34  -0.199
 4  1.08    0.935  -0.641  1.63 
 5  0.711   0.0872  1.27   2.34 
 6 -0.165  -0.663   0.115 -0.374
 7  0.558   0.684  -1.42   0.792
 8  0.188  -1.53    1.00  -0.256
 9  0.896   1.40   -1.15   0.184
10  0.450  -0.911  -1.43   0.885
> output <- vector('double', ncol(df))
> for (i in seq_along(df)) {
+     output[[i]] <- median(df[[i]])
+ }
> output
[1]  0.4248812 -0.2877113 -0.7074765  0.2907293

每个for循环包括3个部分：输出、序列和循环体
输出：output <- vector('double', length(x))
为输出的结果分配足够的空间，如创建给定长度的空向量，用vector()函数，该函数有两个参数：向量类型（”logical”、”integer”、”double”、”character”、”list” 等）和向量长度。
序列：i in seq_along(df)
这部分给定哪些值可以用来循环。seq_along()函数和1:length()函数的作用基本相同，但是会更安全。这里就相当于为df数据框具体列的位置做了标识。
循环体：output[[i]] <- median(df[[i]])
这里是对不同的i进行重复运算，并将每一个结果保存到output的向量空间中。注意这里使用的是[[而不是[，甚至在原子向量中最好也使用[[，因为它可以明确表示我们要处理的是单个元素。

如果想生成一个数据框，可以先将每次迭代结果保存在列表中，再使用dplyr::bind_cols(output)将结果组合成数据框。
【例子】分别使用μ= -10、0、10 和100 的正态分布生成10 个随机数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
> u <- c(-10, 0, 10, 100)
> result <- vector('list', length(u))
> for (i in seq_along(u)) {
+     result[[i]] <- rnorm(10, u[[i]])
+ }
> bind_cols(result)
# A tibble: 10 x 4
       V1     V2    V3    V4
    <dbl>  <dbl> <dbl> <dbl>
 1  -9.37 -1.21   8.15  99.3
 2  -9.75 -1.08   9.29  98.3
 3 -10.6   1.65   9.99 101. 
 4 -11.2  -0.188  9.45  99.9
 5  -9.26 -1.15  10.4  101. 
 6  -8.74 -0.342 10.7  101. 
 7 -10.3   0.987  9.09 102. 
 8 -10.7  -0.152  9.18 100. 
 9  -7.77  0.292 10.9  101. 
10 -10.1   1.63   8.76 101.

当不知道结果要输出的长度时，可以先将结果保存在一个列表中，循环结束后再组合成一个向量：
1
2
3
4
5
6
7
8
9
10
11
12
13
> means <- c(0, 1, 2)
> out <- vector('list', length(means))
> for (i in seq_along(means)) {
+     n <- sample(100, 1)
+     out[[i]] <- rnorm(n, means[[i]])
+ }
> str(out)
List of 3
 $ : num [1:82] 0.634 -0.458 -0.765 0.881 0.12 ...
 $ : num [1:15] 1.904 1.304 4.436 0.193 0.241 ...
 $ : num [1:78] 1.741 3.94 2.297 2.451 0.466 ...
> str(unlist(out))
 num [1:175] 0.634 -0.458 -0.765 0.881 0.12 ...

这里的n是每次在100以下的数当中随机抽取一个数，这样每次rnrom(n, means[[i]])正态分布所产生的随机数个数就不一样了，比如第一次是82个数，第二次是15个数，第三次是78个数。因为结果是随机产生的，所以事先并不知道要输出的长度是多少。这里我们使用了unlist()函数将一个向量列表转换为单个向量，因为列表的长度不同，所以这里不能转换为tibble数据框。

3.1.2 while循环

与for循环的区别在于终止的条件，for循环的终止条件是循环的次数，而while循环的终止条件是达到某一个标准。如计算1到100所有奇数的和：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#for循环
> x <- 0
> for (i in 1:100) {
+     if (i %%2 != 0) {
+         x <- x + i
+     }
+ }
> print(x)
[1] 2500
#while循环：
> x <- 0
> i <- 1
> while(i < 100) {
+     if (i %% 2 != 0) {
+         x <- x + i
+     }
+     i <- i + 1
+ }
#实际上计算奇数之和只需要一条代码：
> sum(seq(1, 100, by = 2))
[1] 2500

也就是说，当事先不知道序列的长度（或者说迭代次数）时，就要使用while循环。这种情况在模拟时很常见，例如，在抛硬币时，想要找出连续3次掷出正面向上的硬币所需要的投掷次数：
1
2
3
4
5
6
7
8
9
10
11
12
13
> flip <- function() sample(c('T', 'H'), 1)
> flips <- 0
> mheads <- 0
> while (mheads < 3) {
+     if (flip() == 'H') {
+         mheads <- mheads + 1
+     } else {
+         mheads <- 0
+     }
+     flips <- flips + 1
+ }
> flips
[1] 21

while 循环比for 循环更常用，因为任何for 循环都可以使用while 循环重新实现，但不是所有while 循环都能使用for 循环重新实现：

3.2 函数式编程

可以将循环包装在函数中，然后再调用这个函数，而不是直接使用循环。例如还是上面那个df，可以将计算每列均值的for循环转换成一个函数，如果还需要计算中位数和标准差，也可以通过拓展代码完成相同的操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
> col_mean <- function(df) {
+     output <- vector('double', length(df))
+     for (i in seq_along(df)) {
+         output[[i]] <- mean(df[[i]])
+     }
+     output
+ }
> col_mean(df)
[1]  0.2935597 -0.1553705 -0.3510391  0.5061221
> col_summary <- function(df, fun) {
+     out <- vector('double', length(df))
+     for (i in seq_along(df)) {
+         out[[i]] <- fun(df[[i]])
+     }
+     return(out)
+ }
> col_summary(df, median)
[1]  0.4248812 -0.2877113 -0.7074765  0.2907293

函数式编程最大的特点在于可以输入和输出函数，上面的例子以及R基础包中的应用函数族（apply()、lapply()、tapply()等）就是将函数作为输入参数。输出函数则相当于生产出了其他函数，称之为工厂函数（Factory function）或闭包（Closure）。下面是输出函数的例子：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
SdFunc2 <- function(func, type) {
+     stopifnot(is.function(func),
+               type %in% c('sample', 'population'))
+     function(x) {
+         stopifnot(is.numeric(x), length(x) > 0)
+         x <- x[!is.na(x)]
+         n <- length(x)
+         m <- func(x)
+         if (type == 'sample') n <- n-1
+         sd <- sqrt(sum((x - m) ^ 2) / (n))
+         return(sd)
+     }
+ }
> SdMean2 <- SdFunc2(func = mean, type = 'sample')
> SdMed2 <- SdFunc2(func = median, type = 'sample')
> x <- sample(100, 30)
> SdMean2(x)
[1] 27.46609
> SdMed2(x)
[1] 27.95162

4 循环的代替

purrr包中提供了一些其他函数，可以对for循环进行抽象。最主要也使用最多的是映射函数，其他的还有预测函数、归约与累计函数等。

4.1 映射函数

4.1.1 单参数映射

将函数作为参数传入另一个函数的做法很强大，但是由于R语言更强大，所以它提供的purrr包里面的函数可以替代很多常见的for循环应用，从而实现向量化计算：
map() 用于输出列表
map_lgl() 用于输出逻辑型向量
map_int() 用于输出整型向量
map_dbl() 用于输出双精度型向量
map_chr() 用于输出字符串型向量
每个函数都使用一个向量作为输入，并对向量里的每一个元素应用一个函数，然后返回和输入向量同样长度（同样名称）的一个新向量。向量的类型由映射函数的后缀决定。

map_()和col_summary()具有以下几点区别：
-所有purrr函数都是用C实现的，速度非常快但是牺牲了可读性。
-第二个参数（即.f，要应用的函数）可以是一个公式、一个字符向量或一个整型向量。
-map_() 使用 … 向.f 传递一些附加的参数，供其在每次调用时使用。
-映射函数还可以保留名称。

1
2
3
4
5
6
7
8
9
10
> map_dbl(df, median)
         a          b          c          d 
 0.4248812 -0.2877113 -0.7074765  0.2907293 
> map_dbl(df, mean, trim = 0.5)
         a          b          c          d 
 0.4248812 -0.2877113 -0.7074765  0.2907293 
> z <- list(x = 1:3, y = 4:5)
> map_int(z, length)
x y 
3 2

4.1.2 多参数映射

上面的函数是对单个输入进行映射，如果需要输入多个参数进行同步迭代，则可以使用map2()和pmap()函数。
例如想模拟几个均值不同、标准差也不同的随机正态分布，这里注意，每次调用时值发生变化的参数（这里是mu 和sigma）要放在映射函数（这里是rnorm）的前面，值保持不变的参数（这里是n）要放在映射函数的后面：

1
2
3
4
5
6
7
> mu <- list(5, 10, -3)
> sigma <- list(1, 5, 10)
> str(map2(mu, sigma, rnorm, n = 5))
List of 3
 $ : num [1:5] 5.79 4.56 6.48 4.75 3.61
 $ : num [1:5] 13.92 12.06 13.26 15.91 7.78
 $ : num [1:5] -4.81 -2.97 -3.63 3.56 -10.35

如果需要接受两个以上的输入，则可以使用pmap()函数。例如生成均值、标准差和样本数量都不相同的正态分布，这里要注意：如果没有为列表的元素命名，那么pmap() 在调用函数时就会按照位置匹配。这样做比较容易出错，而且会让代码的可读性变差，因此最好使用命名参数：
1
2
3
4
5
6
7
> n <- list(1, 3, 5)
> args1 <- list(mean = mu, sd = sigma, n = n)
> str(pmap(args1, rnorm))
List of 3
 $ : num 4.91
 $ : num [1:3] 8.63 9.94 9.57
 $ : num [1:5] 3.04 16.48 -1.04 5.06 1.7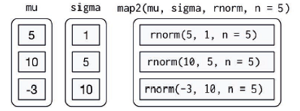

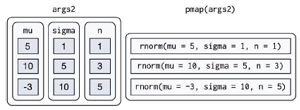
调用不同函数

还有一种更复杂的情况：不但传给函数的参数不同，甚至函数本身也是不同的，这时候用invoke_map()函数。如果输入的参数长度相同，可以将各个参数保存在一个数据框中（上面的情况也是一样）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
> f <- c('runif', 'rnorm', 'rpois')
> param <- list(
+     list(min = -1, max = 1),
+     list(sd = 5),
+     list(lambda = 10)
+ )
> str(invoke_map(f, param, n = 5))
List of 3
 $ : num [1:5] -0.6 0.669 0.283 -0.542 -0.217
 $ : num [1:5] 7.01 4.25 -7.65 -7.43 3.84
 $ : int [1:5] 9 11 11 9 17
#用tribble()函数将参数保存在一个数据框中
> sim <- tribble(
+     ~f, ~params,
+     'runif', list(min = -1, max = 1),
+     'rnorm', list(sd = 5),
+     'rpois', list(lambda = 10)
+ )
> sim %>%
+     mutate(sim = invoke_map(f, params, n = 10))
# A tibble: 3 x 3
  f     params           sim       
  <chr> <list>           <list>    
1 runif <named list [2]> <dbl [10]>
2 rnorm <named list [1]> <dbl [10]>
3 rpois <named list [1]> <int [10]>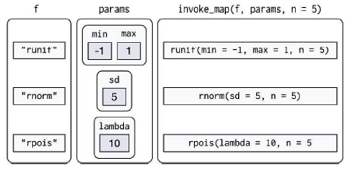

4.2 for循环的其他模式

4.2.1 预测函数

keep()和discard()函数可以分别保留输入中预测值为TRUE 和FALSE 的元素。
some()和every()函数分别用来确定预测值是否对某个元素为真以及是否对所有元素为真。
detect()函数找出预测值为真的第一个元素，detect_index()函数则可以返回这个元素的位置。
head_while()和tail_while()分别从向量的开头和结尾找出预测值为真的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
> iris %>% 
+     keep(is.factor) %>%
+     str()
'data.frame':	150 obs. of  1 variable:
 $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
> iris %>%
+     discard(is.factor) %>%
+     str()
'data.frame':	150 obs. of  4 variables:
 $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...

> x <- list(1:5, letters, list(10))
> x %>% some(is_character)
[1] TRUE
> x %>% every(is_vector)
[1] TRUE

> x <- sample(10)
> x
 [1]  6  9  5  2 10  7  4  1  3  8
> x %>% detect(~ . > 5)
[1] 6
> x %>% detect_index(~ . > 5)
[1] 1

> x %>% head_while(~ . > 5)
[1] 6 9
> x %>% tail_while(~ . > 5)
[1] 8

4.2.2 归约与累计

reduce()函数使用一个“二元”函数（即具有两个基本输入的函数），将其不断应用于一个列表，直到最后只剩下一个元素为止。例如想要通过不断将两个数据框连接成一个的方式来最终生成一个数据框，或者想要找出一张向量列表中的向量间的交集，见代码。
累计函数accumulate()与归约函数很相似，但前者会保留所有中间结果。可以用来实现累计求和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
> dfs <- list(
+     age = tibble(name = "John", age = 30),
+     sex = tibble(name = c("John", "Mary"), sex = c("M", "F")),
+     trt = tibble(name = "Mary", treatment = "A")
+ )
> dfs %>% reduce(full_join)
Joining, by = "name"
Joining, by = "name"
# A tibble: 2 x 4
  name    age sex   treatment
  <chr> <dbl> <chr> <chr>    
1 John     30 M     NA       
2 Mary     NA F     A        
> vs <- list(
+     c(1, 3, 5, 6, 10),
+     c(1, 2, 3, 7, 8, 10),
+     c(1, 2, 3, 4, 8, 9, 10)
+ )
> vs %>%reduce(intersect)
[1]  1  3 10

> x
 [1] 10  5  1  9  7  3  8  6  4  2
> x %>% accumulate(`+`)   #这里注意是反引号
 [1] 10 15 16 25 32 35 43 49 53 55

写在最后

应该尽量避免使用循环，而多使用向量化计算方法，如果必须要使用循环，则需事先定义好变量。使用向量化计算的前提是不同的计算步骤要相互独立。但有些情况下，不同的计算步骤是相互依赖的，此时则需要使用循环来迭代计算，例如计算fibonacci数值：

1
2
3
4
5
6
7
8
9
10
11
#找到10000以下的斐波那契数列
> i <- 2
> x <- 1:2
> while(x[i] < 1e4) {
+     x[i+1] <- x[i-1] + x[i]
+     i <- i + 1
+ }
> x <- x[-i]
> x
 [1]    1    2    3    5    8   13   21   34   55   89  144  233  377  610  987
[16] 1597 2584 4181 6765

  • 本笔记参考书目：Hadley Wickham的《R数据科学》以及李舰&肖凯的《数据科学中的r语言》
赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

愿一生<br><br>温暖纯良<br>不舍爱与自由