支持向量机是借助最优化方法来解决机器学习问题的新工具,建立在统计学理论的VC维理论和结构风险最小原理基础之上,根据有限样本在模型的复杂性和学习能力之间寻求最佳折中。它在解决小样本、非线性及高维度模式识别中表现出许多优势,并能推广应用到函数拟合等其他机器学习问题中。
1 算法简述
该算法相对于其他算法具有更好的预测准确率,主要是因为它可以将低维线性不可分的空间转换为高维的线性可分空间。思想是利用某些支持向量所构成的“超平面”,将不同类别(如线性可分、近似线性可分和非线性可分)的样本点进行划分。如果样本点是非线性可分,就借助核函数技术,实现样本在核空间下完成线性可分的操作。关于“超平面”该如何构造是一个非常复杂的问题,本学渣表示还需要继续深入学习=.=。
支持向量机是一种努力使得结构风险最小化的算法。在机器学习领域中,所谓风险指的是近似模型与真实模型之间的误差。最直观的想法是使用分类器在样本数据上的分类结果与真实结果之间的差值来表示,这个差值统计上称之为经验风险。另外还有一个置信风险,代表了我们再多大程度上可以信任分类器在未知样本上的分类结果。而结构风险最小化,就是寻求经验风险和置信风险之和最小化。
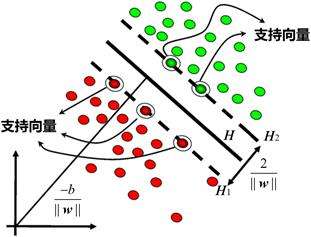
支持向量机的其他概念还有函数间隔、几何间隔,其中涉及大量的统计知识这里就不写出来了(学渣落泪T_T)。不过这里怎么能跳过最基本的概念——支持向量呢!支持向量其实是指真正发挥作用的数据点,也就是到达决策方程距离最小的点(边界点),就是支持向量机的优化目标——找到一个条线使得离该线最近的点能够最远(即边际最大)——的那个点。如下图:
2 在R中的实现
软件包e1071 主要用于支持向量机的模型构建,核心函数svm()的基本使用格式有两种:svm(formula, data = NULL, ..., subset, na.action =na.omit, scale = TRUE) 或svm(x, y = NULL, scale = TRUE, type = NULL, kernel ="radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x) , ..., class.weights = NULL, ...)
根据结果变量的类型,支持向量机模型可以分为分类模型、回归模型或异常检测模型:
如果结果变量为定性变量,则生成分类模型,有C-classification、nu-classification、one-classification三种;
如果结果变量为连续变量,则生成回归模型,有eps-regression、nu-regression两种。
kernel参数有4个可选核函数:线性核函数(linear)、多项式核函数(polynomial)、径向基核函数/高斯核函数(radial basis)以及神经网络核函数(sigmoid)。其中,识别率最高、性能最好的是高斯核函数,其次是多项式核函数,最差的是神经网络核函数。
3 数据集
用的是熟悉的iris数据集:1
2
3
4
5
6
7
8
9
10> library(e1071)
> data("iris")
> summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
结果标签setosa、versicolor、virgiuica 是莺尾花属的三种花的类别。本数据采集了这三种花的四项基本特征,分别为:花萼的长度、花萼的宽度、花瓣的长度以及花瓣的宽度。
4 案例应用
4.1 建立模型
下面分别使用两种方法构建模型以及输出结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25#根据既定公式建立模型
> model = svm(Species~., data = iris)
#根据所给的数据集建立模型
> x = iris[, -5]
> y = iris[, 5]
> model = svm(x, y, kernel = 'radial', gamma = if (is.vector(x)) 1 else 1 / ncol(x))
> summary(model)
Call:
svm.default(x = x, y = y, kernel = "radial", gamma = if (is.vector(x)) 1 else 1/ncol(x))
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
Number of Support Vectors: 51
( 8 22 21 )
Number of Classes: 3
Levels:
setosa versicolor virginica
结果说明该模型的类别为C分类模型,使用的是高斯核函数,cost项目说明本模型确定的约束违反成本为1,且对于该数据,模型找到了51个支持向量,三个类别分别有8、22、21个支持向量。
4.2 预测判别
1 | #确认需要进行预测的样本特征矩阵 |
从混淆矩阵可以看出只有4个样本没有预测正确。
4.3 综合建模
接下来根据3种支持向量分类机和4种核函数,找出最优的参数组合,建立判别结果最优的模型:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28> attach(iris)
> x = subset(iris, select = -Species)
> y = Species
#确定将要使用的分类方式
> type = c('C-classification', 'nu-classification', 'one-classification')
#确定将要使用的核函数
> kernel = c('linear', 'polynomial', 'radial', 'sigmoid')
#初始化预测结果矩阵
> pred = array(0, dim = c(150, 3, 4))
#初始化模型精准度矩阵
> accuracy = matrix(0, 3, 4)
#为方便模型精度计算,将结果变量数量化为1,2,3
> yy = as.integer(y)
> for (i in 1:3) {
+ for (j in 1:4) {
+ pred[, i, j] = predict(svm(x, y, type = type[i], kernel = kernel[j]), x)
+ #因为三种分类方式的模型预测精度计算方式不同,所以分别计算
+ if (i > 2) accuracy[i, j] = sum(pred[, i, j] != 1)
+ else accuracy[i, j] = sum(pred[, i, j] != yy)
+ }
+ }
#确定模型精度变量的行名和列名
> dimnames(accuracy) = list(type, kernel)
> accuracy
linear polynomial radial sigmoid
C-classification 5 7 4 17
nu-classification 5 14 5 12
one-classification 102 75 76 75
程序中accur代表的是模型预测错误的个数。结果得到12个模型所对应的预测精度,其中可以发现C-classification和高斯核函数结合的模型判别错误最少,仅为4个,因此可以选择该组合方式建立模型,其预测结果如下:1
2
3
4
5
6> table(pred[, 1, 3], y)
y
setosa versicolor virginica
1 50 0 0
2 0 48 2
3 0 2 48
4.4 可视化分析
接下来对降维后模型各类别的分布情况和对模型中任意两个特征向量的分布情况进行绘图:1
2
3
4
5
6
7
8
9
10
11
12#降维之后的各类别图像
> plot(cmdscale(dist(iris[, -5])),
+ col = c('red', 'blue', 'green')[as.integer(iris[, 5])],
+ pch = c('o', '+')[1:150 %in% model$index + 1])
> legend(1.8, -0.6, c('setosa', 'versicolor', 'virginica'),
+ col = c('red', 'blue', 'green'), lty = 1, cex = 0.5)
#模型中任意两个特征向量的分布情况
> plot(model, iris, Petal.Width ~ Petal.Length, fill = FALSE,
+ symbolPalette = c('red', 'blue', 'green'), svSymbol = '+')
> legend(1, 2.5, c('setosa', 'versicolor', 'virginica'),
+ col = c('red', 'blue', 'green'), lty = 1, cex = 0.5)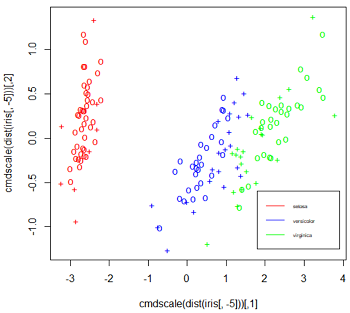
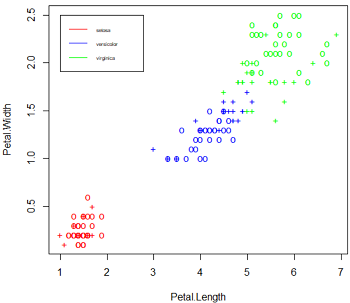
左图为对模型数据类别的一个总观察,图中的“+”表示的是支持向量机,“o”表示的是普通样本点。莺尾属中的第一种setosa类别同其他两种区别较大,而剩下的versicolor类别和virginjca类别却相差很小,甚至存在交叉难以区分,这也解释了模型预测中出现的误判问题。右图为在维度Width与Length下各类别分布情况,同样,setosa类别的花瓣同另外两个类别相差较大,而versicolor类别的花瓣同virginica类别的花瓣相差较小。
4.5 优化建模
针对上面得到的存在类别交叉的情况,可以通过改变模型各类别的比重来对模型进行调整。由于类别setosa同其他两个类别的相差较大,所以可以考虑降低类别setosa在模型中的比重,而提高另外两个类别的比重,即适当牺牲类别setosa的精度来提高其他两个类别的精度。这通过svm()函数中的class.weights参数进行调整,该参数所需要的数据必须为向量,并且具有列名。
当各类别比重相等的时候,即模型为最原始的模型,预测效果可见之前的结果;将versicolor类别和virginjca类别的比重扩大100倍和500倍的情况如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28#各类别比重相等
> wts = c(1, 1, 1)
> names(wts) = c('setosa', 'versicolor', 'virginica')
> model = svm(x, y, class.weights = wts)
#versicolor类别和virginjca类别的比重扩大100倍
> wts1 = c(1, 100, 100)
> names(wts1) = c('setosa', 'versicolor', 'virginica')
> model1 = svm(x, y, class.weights = wts1)
> pred1 = predict(model1, x)
> table(pred1, y)
y
pred1 setosa versicolor virginica
setosa 50 0 0
versicolor 0 49 1
virginica 0 1 49
#versicolor类别和virginjca类别的比重扩大500倍
> wts2 = c(1, 500, 500)
> names(wts2) = c('setosa', 'versicolor', 'virginica')
> model2 = svm(x, y, class.weights = wts2)
> pred2 = predict(model2, x)
> table(pred2, y)
y
pred2 setosa versicolor virginica
setosa 50 0 0
versicolor 0 50 0
virginica 0 0 50
可以看到,通过调整权重后,支持向量机能够将所有样本全部预测正确。所以在实际构建模型的过程中,在必要的时候可以通过改变各类别样本之间的权重比例来提高模型的预测精度。
- 本笔记基于黄文和王正林编著的《数据挖掘:R语言实战》整理

