随机森林算法的实质是基于决策树的分类器集成算法,其中每棵树都依赖于一个随机向量,森林中所有向量都是独立同分布的。随机森林在运算量没有显著提高的前提下提高了预测精度,其对多元共线性不敏感,结果对缺失数据和非平衡的数据比较稳健,可以很好地预测达到多达几千个解释变量。
1 算法概述
随机森林是通过自助法(boot-strap)重采样技术,从原始训练样本集N中有放回地重复随机抽取k个样本生成新的训练集样本集合,然后根据自助样本集生成k个决策树组成的随机森林,新数据的分类结果按决策树多少形成的分数而定。每次抽样生成的袋外数据(out-of-bag,简称OOB)被用来预测分类的正确率,对每次预测结果进行汇总得到错误率的OOB估计,然后评估组合分类的正确率。此外,每一棵决策树所应用的变量也是从所有变量M中随机选取,随机森林通过在每个节点处随机选择特征进行分支,最小化了各决策树之间的相关性,从而提高了分类精确度。
重要参数
1) 随机森林分类性能得主要因素
-单棵树的分类强度:强度越大,整体随机森林的分类性能越好
-树之间的相关度:相关度越大,随机森林的分类性能越差
2) 随机森林的两个重要参数
-树节点预选的变量个数
-随机森林中树的个数
2 在R中的实现
randomForest软件包主要有5个函数:
1) randomForest():建立随机森林模型,既可以建立判别模型,也可以建立回归模型,还可以建立无监督模型;randomForest(formu1a, data=NULL, ..., subset, na.action=na.fail)或randomForest(x, y=NULL, xtest=NULL, ytest=NULL, ntree=500 ,mtry...)
如果响应变量为连续变量,则生成回归模型,预测结果为每棵决策树结果进行平均得到;
如果响应变量为定性变量,则生成判别模型,预测结果为每棵决策树的决策出现概率最大的结果;
如果不设定响应变量的取值,则生成无监督模型,该模型主要用于文本分析以及文本分类。
2) importance():提取在利用函数randomForest()建立模型过程中各个变量的重要性度量结果;importance(x, type=NULL, class=NULL, sca1e=TRUE, ...)
其中,参数type在这里指代的是对于变量重要值的度量标准,l 代表采用精度平均减少值作为度量标准;而2代表采用节点不纯度平均减少值作为度量标准。
3) MDSplot():绘制在建立模型过程中所产生的临近矩阵经过标准化后的坐标图,即不同维度下各个样本点的分布情况。MDSplot(rf, fac, k=2, palette=NULL, pch=20, ...)
4) rflmpute():对数据中的缺失值进行插值;rflmpute (x, y, iter=5, ntree=300, ...) 或 rflmpute(x, data, ..., subset)
参数y在这里为响应变量向量,y不能存在缺失值。
5) treesize():查看随机森林模型中每一棵树所具有的节点个数;treesize(x, terminal=TRUE)
参数terminal主要用于决定节点的计数方式,如果值为默认值TRUE,则将只计算最终根节点数目,如果值FALSE,则将所有的节点全部计数。该函数通常与函数hist()结合使用,绘制相关的柱状图。
3 数据集
本数据采集了白酒品质的11 项基本特征,分别为:非挥发性酸、挥发性酸、拧攘酸、剩余糖分、氧化物、游离二氧化硫、总二氧化硫、密度、酸性、硫酸盐、酒精度。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26> wine = read.csv('wine.csv', header = TRUE, sep = ';')
> dim(wine)
[1] 4898 12
> summary(wine)
fixed.acidity volatile.acidity citric.acid residual.sugar
Min. : 3.800 Min. :0.0800 Min. :0.0000 Min. : 0.600
1st Qu.: 6.300 1st Qu.:0.2100 1st Qu.:0.2700 1st Qu.: 1.700
Median : 6.800 Median :0.2600 Median :0.3200 Median : 5.200
Mean : 6.855 Mean :0.2782 Mean :0.3342 Mean : 6.391
3rd Qu.: 7.300 3rd Qu.:0.3200 3rd Qu.:0.3900 3rd Qu.: 9.900
Max. :14.200 Max. :1.1000 Max. :1.6600 Max. :65.800
chlorides free.sulfur.dioxide total.sulfur.dioxide density
Min. :0.00900 Min. : 2.00 Min. : 9.0 Min. :0.9871
1st Qu.:0.03600 1st Qu.: 23.00 1st Qu.:108.0 1st Qu.:0.9917
Median :0.04300 Median : 34.00 Median :134.0 Median :0.9937
Mean :0.04577 Mean : 35.31 Mean :138.4 Mean :0.9940
3rd Qu.:0.05000 3rd Qu.: 46.00 3rd Qu.:167.0 3rd Qu.:0.9961
Max. :0.34600 Max. :289.00 Max. :440.0 Max. :1.0390
pH sulphates alcohol quality
Min. :2.720 Min. :0.2200 Min. : 8.00 Min. :3.000
1st Qu.:3.090 1st Qu.:0.4100 1st Qu.: 9.50 1st Qu.:5.000
Median :3.180 Median :0.4700 Median :10.40 Median :6.000
Mean :3.188 Mean :0.4898 Mean :10.51 Mean :5.878
3rd Qu.:3.280 3rd Qu.:0.5500 3rd Qu.:11.40 3rd Qu.:6.000
Max. :3.820 Max. :1.0800 Max. :14.20 Max. :9.000
> hist(wine$quality)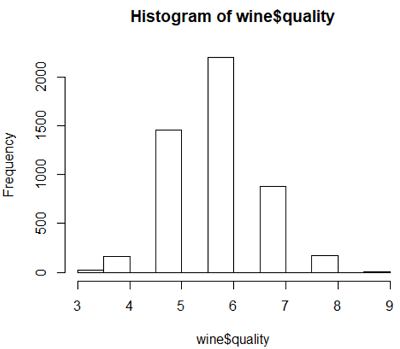
根据结果变量中各等级对应样本量,将白酒品质分为三个等级,其中品质3、4、5对应品质为”bad”,品质6对应品质为”mid”,品质7、8、9对应品质为”good”。1
2
3
4
5
6
7
8
9
10> cha = 0
> for (i in 1:4898) {
+ if (wine[i, 12] > 6) cha[i] = 'good'
+ else if (wine[i, 12] == 6) cha[i] = 'mid'
+ else cha[i] = 'bad'
+ }
> wine[, 12] = factor(cha)
> summary(wine$quality)
bad good mid
1640 1060 2198
4 案例应用
4.1 建立模型
下面分别使用两种方法构建随机森林模型:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15#根据既定公式建立模型
> set.seed(71)
> samp = sample(1:4898, 3000)
> set.seed(111)
> wine_rf = randomForest(quality~., data = wine, importance = TRUE, proximity = TRUE, ntree = 500, subset = samp)
#根据所给的数据集建立模型
#提取wine数据集中除quality列以外的数据作为自交量
> x = subset(wine, select = -quality)
> y = wine$quality
> set.seed(71)
> samp = sample(1:4898, 3000)
> xr = x[samp, ]; yr = y[samp]
> set.seed(111)
> wine.rf = randomForest(xr, yr, importance = TRUE, proximity = TRUE, ntree = 500)
在前文的随机森林模型构建过程中,都会出现set.seed()函数。该函数的主要作用是确定随机数生成器的初始值。由于构建随机森林模型需要不断地从样本中进行抽样来建立森林中的每一棵决策树,所以每次随机抽样的结果会不相同。因此在每次进行模型构建之前设置相应的随机数生成器初始值,就保证在每次构建随机森林模型所使用的随机抽样样本是相同的,即保证了每次建立的随机森林模型是一样的。1
2
3
4
5
6
7
8
9
10
11
12
13
14> print(wine_rf)
Call:
randomForest(formula = quality ~ ., data = wine, importance = TRUE, proximity = TRUE, ntree = 500, subset = samp)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 3
OOB estimate of error rate: 30.57%
Confusion matrix:
bad good mid class.error
bad 697 21 283 0.3036963
good 12 392 238 0.3894081
mid 227 136 994 0.2675018
从输出结果可以知道该模型为判别模型,每颗决策树节点处所选择的变量个数为3,且模型总的预测误差为30.57%,具体预测情况可以看混淆矩阵的结果。
接下来看自变量的重要程度:1
2
3
4
5
6
7
8
9
10
11
12
13> importance(wine_rf)
bad good mid MeanDecreaseAccuracy MeanDecreaseGini
fixed 38.39220 38.04701 28.23129 54.35687 138.8276
volatile 60.62095 57.14363 47.73287 81.72092 195.5095
citric 33.95011 37.38719 27.88769 46.44210 149.4469
residual 31.46575 36.43637 35.79771 55.19329 163.2376
chlorides 44.52846 46.47096 27.53577 56.75493 169.0678
free 45.25569 41.41413 34.22959 64.04598 178.9195
total 34.41994 41.26107 27.18189 50.61239 170.5083
density 31.79573 42.52763 32.02053 53.63531 204.5551
PH 33.29907 44.35856 26.93746 51.25421 158.8621
sulphates 31.49062 36.61428 28.59253 50.10378 145.9429
alcohol 66.08129 66.88405 32.11592 82.88410 240.0514
结果列出了所有自变量以及在不同测算标准下计算出的相应自变量的重要值,较高的指标值说明该自变量对模型的判别情况影响较大。
4.2 优化模型
影响随机森林模型的两个主要因素,一是决策树节点分支所选择的变量个数,二是随机森林模型中决策树的数量。所以在构建模型时需要进一步确定最优的参数值。
对决策树节点分支所选择的变量个数的确定,采用逐一增加变量的方法进行建模:1
2
3
4
5
6
7
8
9
10
11> n = ncol(wine) - 1
#设置模型误判率向量初始值
> rate = 1
> for (i in 1:n) {
+ set.seed(222)
+ model = randomForest(quality~., data = wine, mtry = i, importance = TRUE, ntree = 1000)
+ rate[i] = mean(model$err.rate) #计算基于OOB数据的模型误判率均值
+ }
> rate
[1] 0.2658980 0.2632589 0.2612880 0.2637401 0.2653124 0.2640605 0.2667583
[8] 0.2649265 0.2663877 0.2691432 0.2702067
结果显示,当决策树节点分支所选择的变量个数为3时,模型的误判率均值是最低的。
接下来进一步确定模型中的决策树数量,采用模型的可视化进行分析:1
2
3
4
5
6
7> set.seed(222)
> model = randomForest(quality~., data = wine, mtry = 3, importance = TRUE, ntree = 1000)
> plot(model, col = 1:1)
> legend(800, 0.23, 'mid', cex = 0.9, bty = 'n')
> legend(800, 0.29, 'bad', cex = 0.9, bty = 'n')
> legend(800, 0.37, 'good', cex = 0.9, bty = 'n')
> legend(800, 0.26, 'total', cex = 0.9, bty = 'n')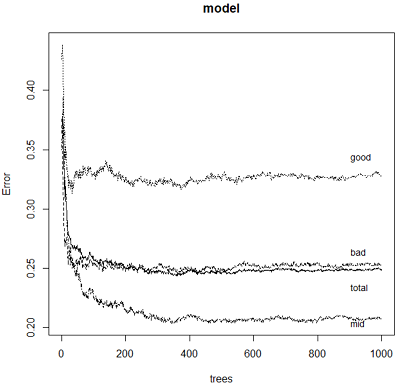
由图中可以看到,当决策树数量大概大于400之后,模型误差趋于稳定,所以最终确定将模型中的决策树数量大致为400左右,以此来达到最优模型。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23> model = randomForest(quality~., data = wine, mtry = 3, proximity = TRUE, importance = TRUE, ntree = 400)
> print(model)
Call:
randomForest(formula = quality ~ ., data = wine, mtry = 3, proximity = TRUE, importance = TRUE, ntree = 400)
Type of random forest: classification
Number of trees: 400
No. of variables tried at each split: 3
OOB estimate of error rate: 24.79%
Confusion matrix:
bad good mid class.error
bad 1229 19 392 0.2506098
good 20 717 323 0.3235849
mid 291 169 1738 0.2092812
#展示随机森林模型中每棵决策树的节点数
> hist(treesize(model))
> min(treesize(model))
[1] 916
> max(treesize(model))
[1] 1023
#展示数据集在二维情况下各类别的具体分布情况
> MDSplot(model, wine$quality, palette = rep(1, 3), pch = as.numeric(wine$quality))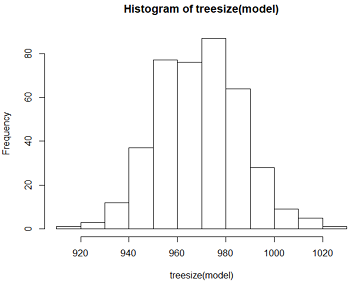
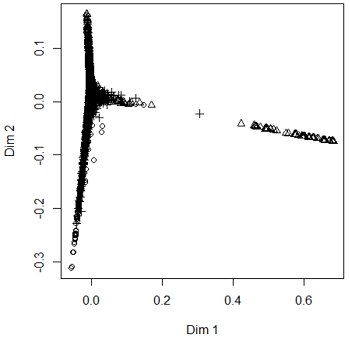
由结果我们可以得到以下信息:
-模型基于OOB数据的总体误判率为24.79%;
-模型中决策树的节点数最少为916,最多的有1023个;
-右上图显示了数据集中的三个类别,三个类别均出现交叉,并且在部分区域,交叉情况较为严重,这同时也解释了模型预测精度较低的原因。
- 本笔记基于黄文和王正林编著的《数据挖掘:R语言实战》整理

