R语言数据挖掘——集成学习

字数统计: 2k字   |   阅读时长: 9分

以民主选举过程来比拟分类器的运作过程，选举中的每位选民的一次投票就相当于一个基分类器的分类结果，而一大批选民的一次投票则可以认为是一个集成分类算法的分类结果。如果有n个基分类器，每个基分类器的预测正确率都为0.5，当用n个基分类器进行共同预测时，预测结果正确的概率则等于“1 — n个基分类器全部预测错误的概率”，即P=1—(1-0.5)^n，即预测正确率渐趋于1。所以将基分类器进行集成的目的是使分类结果稳定，且正确率高。

1 算法概述

集成学习的两个经典算法是：Bagging和AdaBoost。

Bagging是Bootstrap Aggregating的缩写，通过使用bootstrap抽样得到若干个不同的训练集，以这些训练集分别建立模型，即得到一系列基分类器，这些分类器由于来自不同的训练样本，它们对同一测试集的预测效果不一。因此，Bagging算法随后对基分类器的一系列预测结果进行投票（分类问题）或平均（回归问题），从而得到每一个测试集样本的最终预测结果。

AdaBoost相对于Bagging算法更为巧妙，且一般来说是效果更优的集成分类算法，尤其在数据分布不平衡的情况下，其优势更为显著。该算法会根据上一个基分类器对各训练集样本的预测结果，自行调整在本次基分类器构造时，各样本被抽中的概率。具体来说，如果在上一基分类器的预测中，样本 i 被错误分类了，那么在此次基分类器的训练样本抽取过程中，样本 i 就会被赋予较高的权重，以使其能够以较大的可能被抽中，从而提高被正确分类的概率。这种实时调节权重的过程显著提高了集成分类器的稳定性和准确性。

2 在R中的实现

adabag软件包专注于Bagging和Boosting两种算法：
bagging函数：bagging (formula, data, mfinal = 100 , contro1)
boosting函数：boosting(formula, data, boos = TRUE, mfinal = 100, coeflearn = ' Breiman', control)

boosting()中的Adaboost算法以分类树为基分类器，参数mfinal表示算法的迭代次数，即基分类器的个数，可设置为任意整数，缺失值为100，boos参数用于选择在当下的迭代过程中，是否用各观测样本的相应权重来抽取boostrap样本。

3 数据集

该数据集来自于某葡萄牙银行机构的一个基于电话跟踪的商业营销项目，其中收录了包括银行客户个人信息及与电话跟踪咨询结果有关的16个自变量，以及l个因变量一一该客户是否订阅了银行的定期存款。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
> data = read.csv('bank.csv', header = TRUE, sep = ';')
> dim(data)
[1] 4521   17
> summary(data)
      age                 job          marital         education   
 Min.   :19.00   management :969   divorced: 528   primary  : 678  
 1st Qu.:33.00   blue-collar:946   married :2797   secondary:2306  
 Median :39.00   technician :768   single  :1196   tertiary :1350  
 Mean   :41.17   admin.     :478                   unknown  : 187  
 3rd Qu.:49.00   services   :417                                   
 Max.   :87.00   retired    :230                                   
                 (Other)    :713                                   
 default       balance      housing     loan           contact    
 no :4445   Min.   :-3313   no :1962   no :3830   cellular :2896  
 yes:  76   1st Qu.:   69   yes:2559   yes: 691   telephone: 301  
            Median :  444                         unknown  :1324  
            Mean   : 1423                                         
            3rd Qu.: 1480                                         
            Max.   :71188                                         
                                                                  
      day            month         duration       campaign     
 Min.   : 1.00   may    :1398   Min.   :   4   Min.   : 1.000  
 1st Qu.: 9.00   jul    : 706   1st Qu.: 104   1st Qu.: 1.000  
 Median :16.00   aug    : 633   Median : 185   Median : 2.000  
 Mean   :15.92   jun    : 531   Mean   : 264   Mean   : 2.794  
 3rd Qu.:21.00   nov    : 389   3rd Qu.: 329   3rd Qu.: 3.000  
 Max.   :31.00   apr    : 293   Max.   :3025   Max.   :50.000  
                 (Other): 571                                  
     pdays           previous          poutcome      y       
 Min.   : -1.00   Min.   : 0.0000   failure: 490   no :4000  
 1st Qu.: -1.00   1st Qu.: 0.0000   other  : 197   yes: 521  
 Median : -1.00   Median : 0.0000   success: 129             
 Mean   : 39.77   Mean   : 0.5426   unknown:3705             
 3rd Qu.: -1.00   3rd Qu.: 0.0000                            
 Max.   :871.00   Max.   :25.0000 

#构造训练集和测试集
> sub = sample(1:nrow(data), round(nrow(data) / 4))
> length(sub)
[1] 1130
> data_train = data[-sub, ]
> data_test = data[sub, ]
> dim(data_train); dim(data_test)
[1] 3391   17
[1] 1130   17

4 应用案例

4.1 Bagging算法

1
2
3
4
5
6
7
8
> 1ibrary(adabag)
> 1ibrary(rpart)
> bag = bagging(y~., data_train, mfinal = 5)
#通过control参数控制基分类树的复杂度
> bag1 = bagging(y~., data_train, mfinal = 5, control = rpart.control(maxdepth = 3))
> names(bag1)
[1] "formula"    "trees"      "votes"      "prob"       "class"     
[6] "samples"    "importance" "terms"      "call"

4.1.1 训练集的基本情况

简单查看上面输出结果的具体内容：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#模型bag1中第二棵决策树的构成
> bag1$trees[2]
[[1]]
n= 3391 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 3391 366 no (0.89206724 0.10793276)  
   2) duration< 628.5 3125 231 no (0.92608000 0.07392000)  
     4) poutcome=failure,other,unknown 3042 175 no (0.94247206 0.05752794)  
       8) month=apr,aug,dec,feb,jan,jul,jun,may,nov,sep 2983 141 no (0.95273215 0.04726785) *
       9) month=mar,oct 59  25 yes (0.42372881 0.57627119) *
     5) poutcome=success 83  27 yes (0.32530120 0.67469880)  
      10) duration< 146 16   4 no (0.75000000 0.25000000) *
      11) duration>=146 67  15 yes (0.22388060 0.77611940) *
   3) duration>=628.5 266 131 yes (0.49248120 0.50751880)  
     6) month=jan,nov,oct 37   5 no (0.86486486 0.13513514) *
     7) month=apr,aug,dec,feb,jul,jun,may 229  99 yes (0.43231441 0.56768559)  
      14) duration< 790.5 97  42 no (0.56701031 0.43298969) *
      15) duration>=790.5 132  44 yes (0.33333333 0.66666667) *
#模型bag1中第105至第110个样本的投票情况，因为共有5棵决策树，每棵树对每一样本的类别有各自的类别，则总票数为5.
> bag1$votes[105:110, ]
     [,1] [,2]
[1,]    5    0
[2,]    5    0
[3,]    5    0
[4,]    5    0
[5,]    5    0
[6,]    5    0
#模型bag1中第105至第110个样本预测为各类别的概率
> bag1$prob[105:110, ]
      [,1] [,2]
[1,]    1    0
[2,]    1    0
[3,]    1    0
[4,]    1    0
[5,]    1    0
[6,]    1    0
#模型bag1对于第105至第110个样本的预测类别
> bag1$class[105:110]
[1] "no" "no" "no" "no" "no" "no"
#模型bag中各输入变量的相对重要性
> bag1$importance
        age    balance   campaign    contact        day    default 
 0.9077055  0.0000000  0.0000000  1.8540732  0.0000000  0.0000000 
  duration  education    housing        job       loan    marital 
57.9747707  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000 
     month      pdays   poutcome   previous 
 8.6889082  0.5551839 30.0193586  0.0000000

这里用一下决策树章节没机会用到的函数，把上面这棵树画一下：
1
2
> tree = bag1$trees[[2]]
> rpart.plot(tree, type = 4)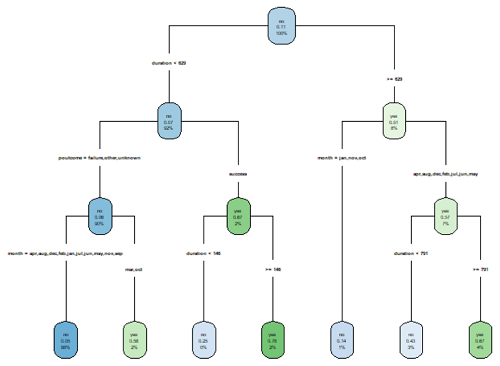

可以看到，效果并不是很好=.=，字太小看不清楚，不过其他函数画出来的也一言难尽……

4.1.2 对测试集的目标变量进行预测

1
2
3
4
5
6
7
8
9
10
11
12
> pre_bag = predict(bag, data_test)
> names(pre_bag)
[1] "formula"   "votes"     "prob"      "class"     "confusion" "error"    
#测试集预测结果的混淆矩阵
> pre_bag$confusion
               Observed Class
Predicted Class  no yes
            no  977  78
            yes  28  47
#测试集预测错误率
> pre_bag$error
[1] 0.09380531

下面计算测试集总体的预测错误率，以及“yes”类和“no”类各自的错误率：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
> sub_minor = which(data_test$y == 'yes')
> sub_major= which(data_test$y == 'no')
> length(sub_minor); length(sub_major)
[1] 125
[1] 1005
#计算总体错误率
> err_bag = sum(pre_bag$class != data_test$y) / nrow(data_test)
#计算少数类"yes"的错误率
> err_minor_bag = sum(pre_bag$class[sub_minor] != data_test$y[sub_minor]) / length(sub_minor)
#计算多数类"no"的错误率
> err_major_bag = sum(pre_bag$class[sub_major] != data_test$y[sub_major]) / length(sub_major)
> err_bag; err_major_bag; err_minor_bag
[1] 0.09380531
[1] 0.0278607
[1] 0.624

可以看到总体错误率约为0.0938，多数类“no”的错误率比少数类“yes”的错误率要低，仅为0.0278，这正是由于数据的不平衡性造成的。而AdaBoost算法在处理不平衡数据集具有一定优势。

4.2 AdaBoost算法

1
2
3
4
5
6
7
8
9
10
> boo = boosting(y~., data_train, mfinal = 5)
> pre_boo = predict(boo, data_test)
#计算三类错误率
> err_boo = sum(pre_boo$class != data_test$y) / nrow(data_test)
> err_minor_boo = sum(pre_boo$class[sub_minor] != data_test$y[sub_minor]) / length(sub_minor)
> err_major_boo = sum(pre_boo$class[sub_major] != data_test$y[sub_major]) / length(sub_major)
> err_boo; err_major_boo; err_minor_boo
[1] 0.1106195
[1] 0.04776119
[1] 0.616

AdaBoost算法对比Bagging算法在修正数据集的不平衡问题上有一点点成效，但效果差别不大。仅一次结果可能很难看出两者的差异，且具有偶然性，可以在今后的学习中多积累经验。

  • 本笔记基于黄文和王正林编著的《数据挖掘：R语言实战》整理
赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

愿一生<br><br>温暖纯良<br>不舍爱与自由