判别分析就是根据已掌握的每个类别若干样本的数据信息,总结出客观事物分类的规律性,建立判别公式和判别准则,在遇到新的样本点时,再根据已总结出的判别公式和判别准则,来判断该样本点所属的类别。我个人觉得这应该属于监督学习的分类器算法。
本笔记记录基于R语言的三大主流判别分析算法:
-费尔希判别:包括线性判别分析和二次判别分析
-贝叶斯判别:主要是朴素贝叶斯分类算法
-距离判别:包括K最近邻(kNN)和有权重的K最近邻算法
在R中的实现方式如下图所示:
1 数据准备
选用kknn包的miete数据集,该数据集记录了1994年慕尼黑的住房租金标准中的一些有趣变量,比如房子的面积、是否有浴室、是否有中央供暖、是否供应热水等,这些都影响井决定着租金的高低。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41> library(kknn)
> data("miete")
> head(miete)
nm wfl bj bad0 zh ww0 badkach fenster kueche mvdauer bjkat
1 693.29 50 1971.5 0 1 0 0 0 0 2 4
2 736.60 70 1971.5 0 1 0 0 0 0 26 4
3 732.23 50 1971.5 0 1 0 0 0 0 1 4
4 1295.14 55 1893.0 0 1 0 0 0 0 0 1
5 394.97 46 1957.0 0 0 1 0 0 0 27 3
6 1285.64 94 1971.5 0 1 0 1 0 0 2 4
wflkat nmqm rooms nmkat adr wohn
1 1 13.865800 1 3 2 2
2 2 10.522857 3 3 2 2
3 1 14.644600 1 3 2 2
4 2 23.548000 3 5 2 2
5 1 8.586304 3 1 2 2
6 3 13.677021 4 5 2 2
> dim(miete)
[1] 1082 17
> summary(miete)
nm wfl bj bad0 zh ww0
Min. : 127.1 Min. : 20.00 Min. :1800 0:1051 0:202 0:1022
1st Qu.: 543.6 1st Qu.: 50.25 1st Qu.:1934 1: 31 1:880 1: 60
Median : 746.0 Median : 67.00 Median :1957
Mean : 830.3 Mean : 69.13 Mean :1947
3rd Qu.:1030.0 3rd Qu.: 84.00 3rd Qu.:1972
Max. :3130.0 Max. :250.00 Max. :1992
badkach fenster kueche mvdauer bjkat wflkat nmqm
0:446 0:1024 0:980 Min. : 0.00 1:218 1:271 Min. : 1.573
1:636 1: 58 1:102 1st Qu.: 2.00 2:154 2:513 1st Qu.: 8.864
Median : 6.00 3:341 3:298 Median :12.041
Mean :10.63 4:226 Mean :12.647
3rd Qu.:17.00 5: 79 3rd Qu.:16.135
Max. :82.00 6: 64 Max. :35.245
rooms nmkat adr wohn
Min. :1.000 1:219 1: 25 1: 90
1st Qu.:2.000 2:230 2:1035 2:673
Median :3.000 3:210 3: 22 3:319
Mean :2.635 4:208
3rd Qu.:3.000 5:215
Max. :9.000
去除nm、bj和wflkat这三个变量,并且选择nmkat这个变量(按区间划分的净租金)作为待判别变量,因为该变量在含义上受其他变量的影响,且由输出结果可知,该变量共有5个类等级别,且每一类的样本量都为200多个,分布较为均匀。
该净租金nmkat变量的5个等级的含义依次为: 1表示租金少于500马克,2表示租金介于500和675马克之间,3表示租金介于675和850马克之间,4表示租金介于850和1150马克之间,5表示租金不低1150马克。
接下来对该数据集进行训练集和测试集的划分。为提高判别效果,且nmkat的样本取值在5个等级中分布均匀,因此采用分层抽样对这5个等级抽取等量样本。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38> library(sampling)
#按照训练集占数据总量2/3的比例,计算每一等级中应抽取的样本量
> n = round(2/3 * nrow(miete) / 5)
> n
[1] 144
#以nmkat变量的5个等级划分层次,进行分层抽样
> sub_train = strata(miete, stratanames = 'nmkat', size = rep(n, 5), method = 'srswor')
#显示训练集抽取情况,包括nmkat变量取值、该样本在数据集中的序号、被抽取到的概率,以及所在层次
> head(sub_train)
nmkat ID_unit Prob Stratum
1 3 1 0.6857143 1
3 3 3 0.6857143 1
8 3 8 0.6857143 1
16 3 16 0.6857143 1
20 3 20 0.6857143 1
22 3 22 0.6857143 1
#获取如上ID_unit所对应的样本构成训练集,并剔除变量1 、3 、12
> data_train = miete[sub_train$ID_unit, c(-1, -3, -12)]
#获取除ID_unit所对应样本之外的数据构成测试集,并剔除变量1 、3 、12
> data_test = miete[-sub_train$ID_unit, c(-1, -3, -12)]
> dim(data_train); dim(data_test)
[1] 720 14
[1] 362 14
> head(data_test)
wfl bad0 zh ww0 badkach fenster kueche mvdauer bjkat nmqm rooms
2 70 0 1 0 0 0 0 26 4 10.52286 3
4 55 0 1 0 0 0 0 0 1 23.54800 3
7 28 0 1 0 0 1 1 9 4 17.01107 1
11 75 0 1 0 1 0 1 3 6 16.50453 3
12 83 0 1 0 1 0 1 1 6 14.60277 3
13 50 0 1 0 1 0 0 4 3 10.55080 2
nmkat adr wohn
2 3 2 2
4 5 2 2
7 1 2 2
11 5 2 2
12 5 2 2
13 2 2 2
2 费尔希判别
该判别的基本思想是“投影”,即将高维空间的点向低维空间投影,最重要的是选择出适当的投影轴:保证投影后,使每一类之内的投影值所形成的类内离差尽可能小,而不同类之间的投影值所形成的类间离差尽可能大,即在该空间中有最佳的可分离性。
具体的,对于线性判别,可以先将样本点投影到一维空间,即直线上,若效果不明显,则可以考虑增加一个维度,投影到二维空间中,以此类推;而二次判别与线性判别的区别在于投影面的形状不同,二次判别使用若干二次曲面,而非直线或平面来将样本划分至相应的类别中。因此,二次判别的适用面比线性判别要广。
2.1 线性判别分析
MASS包的lda()函数,根据使用对象,该函数有三种主要格式:
-公式形式:lda(formula, data, ..., subset, na.action)
-数据框形式:lda(x, grouping, prior = proportions, tol, method, CV = FALSE, ...)
-矩阵形式:lda(x, grouping, . .., subset, na.action)
2.1.1 公式formula格式
1 | > library(MASS) |
结果可得执行过程中所使用的先验概率prior、各变量在每一类别中的均值等,也可具体查看其它结果项。
2.1.2 数据框data.frame及矩阵matrix格式
两种函数格式的主体参数都为x与grouping,因此只运行一种:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21> fit_lda2 = lda(data_train[, -12], data_train[, 12])
> fit_lda2
Call:
lda(data_train[, -12], data_train[, 12])
Prior probabilities of groups:
1 2 3 4 5
0.2 0.2 0.2 0.2 0.2
Group means:
wfl bad0 zh ww0 badkach fenster kueche mvdauer
1 55.56944 1.090278 1.534722 1.152778 1.375000 1.090278 1.020833 12.361111
2 59.16667 1.013889 1.798611 1.034722 1.513889 1.076389 1.076389 11.222222
3 66.89583 1.020833 1.840278 1.048611 1.541667 1.055556 1.062500 12.701389
4 73.51389 1.006944 1.875000 1.034722 1.666667 1.041667 1.111111 10.180556
5 92.45833 1.006944 1.944444 1.013889 1.770833 1.034722 1.166667 5.166667
……
Proportion of trace:
LD1 LD2 LD3 LD4
0.9771 0.0183 0.0029 0.0016
2.1.3 判别规则可视化
1 | > plot(fit_lda1) |
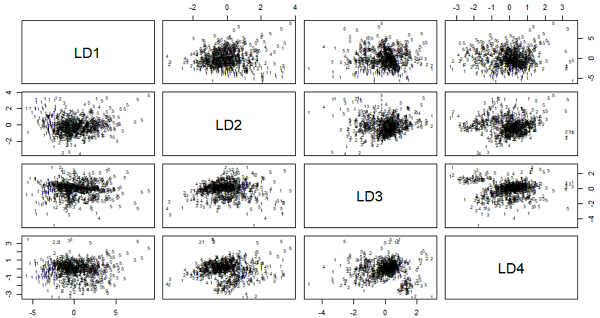
图中可以看到在所有的4个判别式下1至5这5个类别的分布情况,不同类别样本已用相应数字标出。
2.1.4 对测试集待判别变量取值进行预测
1 | > pre_lda1 = predict(fit_lda1, data_test) |
混淆矩阵中,行表示实际的类别,列表示预测判定的类别。在362个测试样本中,实际属于第1类的有75个,而判定为第1类的有47个,24个错判为第2类,3个错判为第3类,1个错判为第4类。其中,第3类的样本被错判的个数最多,共有29个被错误分类,这有可能是类别3与类别2、4的样本之间相似度太高导致的。
2.2 二次判别分析
MASS包的qda()函数,根据使用对象,该函数也有三种主要格式:
-数据框形式:qda(x, grouping, prior = proportions, method, CV = FALSE, nu, .. .)
-公式形式:qda(formula, data, ..., subset, na.action)
-矩阵形式:qda(x, grouping, ..., subset, na.action)
3 贝叶斯判别
利用贝叶斯公式,对给出的待分类样本,求出此样本出现条件下各个类别出现的概率,哪个最大,就认为词样本属于哪个类别。其优势在于不怕噪音和无关变量,不足之处是它假设各特征之间是无关的,而现实中各个特征属性间往往并非独立。
klaR包的NaiveBayes()函数,该函数有两种格式:
-默认情况:NaiveBayes(x, grouping, prior, usekernel = FALSE, fL = 0, ...)
-公式形式:NaiveBayes(formula, data, ..., subset, na.action = na.pass)
这里只展示公式形式。
3.1 公式formula格式
1 | > library(klaR) |
可以看到生成了7项结果,可以通过具体选项进行调用显示。其中table选项储存了用于建立判别规则的所有变量在各类别下的条件概率,这是运行贝叶斯判别算法的一个重要过程。
3.2 各类别下变量密度可视化
以占地面积wfl和每平米净租金nmqm两个变量来查看密度图像:1
2plot(fit_Bayes1, vars = 'wfl', n = 50, col = c(1, 'darkgrey', 1, 'darkgrey', 1))
plot(fit_Bayes1, vars = 'nmqm', n = 50, col = c(1, 'darkgrey', 1, 'darkgrey', 1))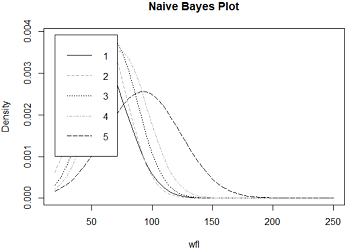
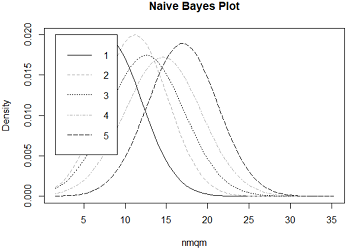
左图是占地面积wfl变量的密度图,5条曲线分别对应5个租金等级,虽然图例挡住了(这个我真的不会调=.=),但是还是可以看到租金等级越大,曲线的最高点越往右移,即所对应的占地面积水平依次提高,也就是说面积越大的房屋租金越高,符合常识。右图也一样,单位租金越高,总租金也越高。
3.3 对测试集待判别变量取值进行预测
1 | > pre_Bayes1 = predict(fit_Bayes1, data_test) |
结果包括各样本的预测类别class和预测过程中各样本属于每一类别的后验概率posterior两项,每一样本属于各类别的后验概率最高者为该样本被判别的类别。如2号样本以0.4128的后验概率最高,被判定为第3类。
同样以混淆矩阵和错误率两种方式来评价贝叶斯判别的预测效果:1
2
3
4
5
6
7
8
9
10
11> table(data_test$nmkat, pre_Bayes1$class)
1 2 3 4 5
1 39 22 10 0 4
2 14 34 24 10 4
3 8 24 19 8 7
4 0 5 17 23 19
5 1 1 0 8 61
> error_Bayes1 = sum(as.numeric(as.numeric(pre_Bayes1$class) != as.numeric(data_test$nmkat))) / nrow(data_test)
> error_Bayes1
[1] 0.5138122
在混淆矩阵中可以看到只有第5类中的大部分样本被正确分类,且预测错误率为51%,可以说判别效果不佳,这很可能是该数据集变量不符合朴素贝叶斯判别执行的前提条件——各变量条件独立,即参与建立判别规则的这些变量是有着较显著的相关性的,这很大程度影响了预测效果的好坏。
4 距离判别
基本思想是根据待判别样本与已知类别样本之间的距离远近做出判别。具体的,即根据已知类别样本信息建立距离判别函数式,再将各待判定样本的属性数据逐一代入式中计算,得到距离值,再据此将样本判入距离值最小的来别的样本簇。
4.1 K最近邻算法
K最近邻算法在进行判别时,由于其主要依靠周围有限近邻样本的信息,而不是靠判别类域的方法来确定所属类别,因此适合类域的交叉或重叠较多的待分样本集。可参考Python部分笔记。
class包的knn()函数:knn(train, test, cl, k = 1, 1 = 0, prob = FALSE, use.all = TRUE),该函数默认选择欧氏距离来寻找所需的k的最近样本。
knn()与下一节的kknn()集判别规则的“建立”和“预测”这两个步骤于一体,即不需要在规则建立后再使用predict()函数进行预测。
按照次序向knn()函数中依次放入训练集中各属性变量(除第12个变量)、测试集(除第12个变量)、训练集的判别变量(第12个变量),并首先取K的默认值1进行判别。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18> library(class)
> fit_pre_knn = knn(data_train[, -12], data_test[, -12], cl = data_train[, 12])
> fit_pre_knn
[1] 3 5 1 5 5 1 5 1 3 1 1 4 4 4 3 2 1 2 3 4 2 5 2 2 1 1 1 3 3 2 2 3
……
[353] 5 2 5 5 2 4 5 3 3 1
Levels: 1 2 3 4 5
> table(data_test$nmkat, fit_pre_knn)
fit_pre_knn
1 2 3 4 5
1 54 15 6 0 0
2 10 45 29 2 0
3 0 14 43 9 0
4 0 1 11 47 5
5 0 1 1 11 58
> error_knn = sum(as.numeric(as.numeric(fit_pre_knn) != as.numeric(data_test$nmkat))) / nrow(data_test)
> error_knn
[1] 0.3176796
混淆矩阵显示nmkat的5个类别分别有54、45、43、47、58个样本被正确分类,第5类被正确分类的样本最多。预测错误率为31.7%,判别效果较前几种算法都要好。
接下来通过调整K的取值,选择出最适合于该数据集的k值,将寻找范围控制在1至20:1
2
3
4
5
6
7
8
9
10
11
12> error_knn = rep(0, 20)
> for (i in 1:20) {
+ fit_pre_knn = knn(data_train[,-12], data_test[,-12], cl=data_train[,12], k=i)
+ error_knn[i] = sum(as.numeric(as.numeric(fit_pre_knn) != as.numeric(data_test$nmkat))) / nrow(data_test)
+ }
> error_knn
[1] 0.3176796 0.3618785 0.3149171 0.3535912 0.3204420 0.3314917
[7] 0.3066298 0.3370166 0.3591160 0.3259669 0.3342541 0.3425414
[13] 0.3370166 0.3646409 0.3674033 0.3618785 0.3729282 0.3618785
[19] 0.3756906 0.3756906
#对20 个错误率作作折线图
> plot(error_knn, type = 'l', xlab = 'k')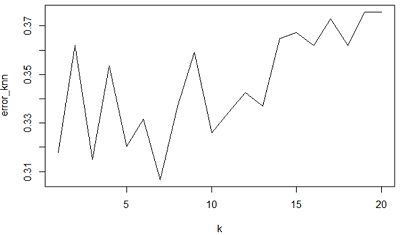
由图中可以清楚地看到,当k取7时预测效果最佳,对应前面的数值结果,错误率仅为30.7%。
K最近邻算法的不足之处在于,当样本不平衡时,即某些类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个最近邻样本中大容量类别的样本占多数。这种情况可以使用有权重的k最近邻算法改进。
4.2 有权重的k最近邻算法
有权重的K最近邻算法在kNN基础上,对各已知类别样本点根据其距离未知样本点的远近,赋予了不同的权重,即距离越近的权重越大。一般来说,加入权重后的kNN算法判别效果更优。
kknn包的kknn()函数:kknn(formu1a = formu1a(train), train, test, na.action = na.omit(), k = 7, distance = 2, kerne1 = "optima1", ykerne1 = NULL, sca1e=TRUE, contrasts = c('unordered' = "contr.dummy", ordered = "contr.ordina1"))
其中参数distance取2为欧氏距离,取l时为曼哈顿距离。
将规则建立公式nmkat~.以及训练集和测试集依次放进函数,设置K为5:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37> library(kknn)
> fit_pre_kknn = kknn(nmkat~., data_train, data_test[, -12], k = 5)
> summary(fit_pre_kknn)
Call:
kknn(formula = nmkat ~ ., train = data_train, test = data_test[, -12], k = 5)
Response: "ordinal"
fit prob.1 prob.2 prob.3 prob.4 prob.5
1 2 0.00000000 0.76636967 0.84709384 1.00000000 1
2 4 0.00000000 0.00000000 0.00000000 0.74185509 1
3 2 0.48513212 0.76636967 1.00000000 1.00000000 1
4 5 0.00000000 0.02451458 0.02451458 0.43414371 1
5 4 0.00000000 0.02451458 0.02451458 0.50964671 1
……
166 3 0.00000000 0.17742074 0.66255287 1.00000000 1
[ reached 'max' / getOption("max.print") -- omitted 196 rows ]
#用fitted()函数输出如上结果的fit(fit记录了某样本最终被判定的类别)
> fit = fitted(fit_pre_kknn)
> fit
[1] 2 4 2 5 4 2 5 1 3 1 3 3 4 4 3 2 1 2 2 4 2 5 4 3 1 1 2 2 2 3 1 4
……
[353] 4 2 5 5 3 4 5 4 3 2
Levels: 1 < 2 < 3 < 4 < 5
#输出混淆矩阵和错误率评价判别结果
> table(data_test$nmkat, fit)
fit
1 2 3 4 5
1 32 28 10 3 2
2 10 36 31 9 0
3 2 15 32 15 2
4 0 3 25 28 8
5 0 1 3 15 52
> error_kknn = sum(as.numeric(as.numeric(fit) != as.numeric(data_test$nmkat))) / nrow(data_test)
> error_kknn
[1] 0.5027624
- 本笔记基于黄文和王正林编著的《数据挖掘:R语言实战》整理

