R语言数据挖掘——聚类分析

2020-03-15

字数统计: 4.7k字 | 阅读时长: 21分

本笔记记录基于R语言的普及性最广、最实用、最具有代表性的5种聚类算法：
-K-均值聚类(K-Means)
-K-中心点聚类(K-Medoids)
-系谱聚类(Hierarchical Clustering, HC)
-密度聚类(Densit-based Spatial Clustering of Application with Noise, DBSCAN)
-期望最大化聚类(Expectation Maximization, EM)

在R中的实现方式如下图所示：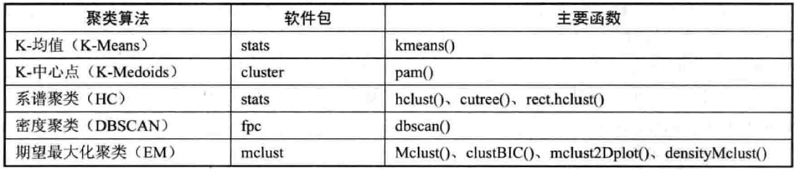

1 数据准备

该数据集含有68个国家和地区的出生率(%)与死亡率(%)。

> countries = read.csv('countries.csv', head = F)
> head(countries)
           V1   V2   V3
1     ALGERIA 36.4 14.6
2       CONGO 37.3  8.0
3       EGYPT 42.1 15.3
4       GHANA 55.8 25.6
5 IVORY COAST 56.1 33.1
6    MALAGASY 41.8 15.8
> names(countries) = c("country", "birth", "death")
> var = countries$country
> var = as.character(var)
> for(i in 1:68) row.names(countries)[i] = var[i]
> head(countries)
                country birth death
ALGERIA         ALGERIA  36.4  14.6
CONGO             CONGO  37.3   8.0
EGYPT             EGYPT  42.1  15.3
GHANA             GHANA  55.8  25.6
IVORY COAST IVORY COAST  56.1  33.1
MALAGASY       MALAGASY  41.8  15.8

接下来选取几个样本点对数据集进行可视化：

#这部分代码最好在脚本完成，别问我为什么知道
> plot(countries$birth, countries$death)
#获取6个国家和地区在数据集中的位置
> C = which(countries$country == "CHINA")
> T = which(countries$country == "TAIWAN")
> H = which(countries$country == "HONG KONG")
> I = which(countries$country == "INDIA")
> U = which(countries$country == "UNITED STATES")
> J = which(countries$country == "JAPAN")
#获取出生率最高的国家在数据集中的位置
> M = which.max(countries$birth)  
#以实心圆点标出如上国家和地区的样本点
> points(countries[c(C,T,H,I,U,J,M),-1], pch = 16) 
#标出6个国家和地区样本点的图例
> legend(countries$birth[C]-1.2, countries$death[C], "CHINA", bty="n", xjust=0, yjust=0.5, cex=0.8)
> legend(countries$birth[T], countries$death[T], "TAIWAN", bty="n", xjust=0.5, cex=0.8)
> legend(countries$birth[H], countries$death[H], "HONG KONG", bty="n", xjust=0.5, cex=0.8)
> legend(countries$birth[I]-1.2,countries$death[I], "INDIA", bty="n", xjust=0, yjust=0.5, cex=0.8)
> legend(countries$birth[U], countries$death[U], "UNITED STATES", bty="n", xjust=0.5, yjust=0, cex=0.8)
> legend(countries$birth[J], countries$death[J], "JAPAN", bty="n", xjust=1, yjust=0.5, cex=0.8)
> legend(countries$birth[M], countries$death[M], countries$country[M], bty="n", xjust=1, cex=0.8)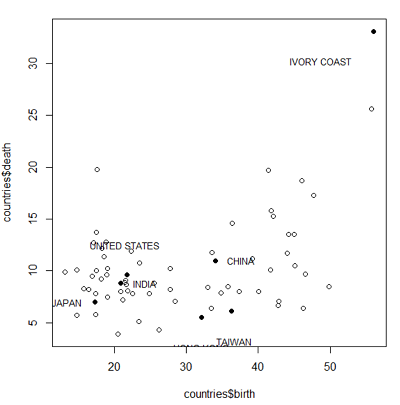

2 聚类分析应用

2.1 K-均值聚类

K-均值聚类是最早出现的聚类分析算法之一，它是一种快速聚类方法，但对于异常值或极值敏感，稳定性差，因此较适合处理分布集中的大样本数据集（可参考Python部分的k-means算法解释）。
调用stats包的kmeans()函数实现：kmeans(x, centers, iter.max=10, nstart=l , algorithm=c("Hartigan-Wong", "Lloyd", "For-gy", "MacQueen"))

在该数据集中，由于事先不知道应该把数据分为几类，因此可通过调节类别参数center的取值，通过组间平方和占总平方和的百分比（即“聚类优度”）来比较选择出最优类别数。由于共有68个样本，可将类别数从1到67取遍：

> library(stats)
#设置result变量用于存放67个聚类优度值
> result = rep(0, 67)
#对类别数K取1到67进行循环
> for (k in 1:67) {
+     fit_km = kmeans(countries[, -1], centers = k)
+     result[k] = fit_km$betweenss / fit_km$totss
+ }
#输出计算所得resu1t ，取小数位后两位的结果
> round(result, 2)
 [1] 0.00 0.72 0.82 0.85 0.86 0.92 0.93 0.93 0.95 0.96 0.96 0.96 0.95 0.97 0.97 
[16] 0.98 0.98 0.98 0.99 0.98 0.97 0.98 0.99 0.98 0.99 0.99 0.99 0.99 0.99 0.99 
[31] 0.99 0.99 0.99 0.99 0.99 1.00 0.99 0.99 0.99 1.00 0.99 0.99 1.00 1.00 1.00 
[46] 1.00 0.99 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 
[61] 1.00 1.00 1.00 1.00 1.00 1.00 1.00

由以上结果大概看出，当类别数约小于10时，随着类别数的增加聚类效果越来越好，但当类别数超过10以后再增加时，聚类效果基本不再提高。
下面对result进行可视化来直观比较各类别数下的聚类优度：

> plot(1:67, result, type='b', main='Choosing the Optimal Number of Cluster', xlab='number of cluster:1 to 67', ylab='brtweenss/totss')
#将类别数为10 的点用实心圆标出
> points(10, result[10], pch=16)
#对类别数为10的点给出其坐标标注(x,y)，x为其类别数10，y为其聚类优度（%）
> legend(10, result[10], paste('(10,',sprintf('%.1f%%',result[10]*100),')',sep=''), bty='n', xjust=0.3, cex=0.8)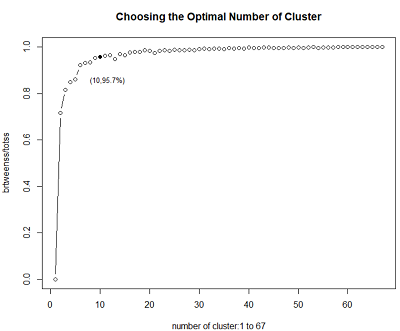

实际上，最优类别数可以是10，也可以是9、11、12等，并无太大差别。在实际选择过程中，如果并非要求极高的聚类效果，取k=5或6即可，较小的类别数在后续的数据分析过程中往往更为方便有效。
接下来对类别数K取10时的聚类结果进行输出：

> fit_km1 = kmeans(countries[, -1], centers = 10)
> print(fit_km1)
K-means clustering with 10 clusters of sizes 5, 9, 2, 1, 7, 7, 6, 9, 11, 11

Cluster means:
      birth     death
1  18.32000  6.400000
2  18.17778 11.311111
3  55.95000 29.350000
4  17.60000 19.800000
5  26.24286  7.357143
6  44.04286 16.257143
7  15.28333  8.616667
8  44.37778  8.744444
9  21.75455  8.990909
10 35.09091  9.036364

Clustering vector:
       ALGERIA          CONGO          EGYPT          GHANA    IVORY COAST 
            10             10              6              3              3 
      MALAGASY        MOROCCO        TUNISIA       CAMBODIA         CEYLON 
             6              6              8              6             10 
         CHINA         TAIWAN      HONG KONG          INDIA      INDONESIA 
            10             10             10              9              5 
          IRAQ          JAPAN         JORDAN          KOREA       MALAYSIA 
             1              1              8              7             10 
      MONGOLIA   PHILLLIPINES          SYRIA       THAILAND        VIETNAM 
            10              5              5             10              5 
        CANADA     COSTA RICA     DOMINICANR      GUATEMALA       HONDURAS 
             5              8             10              6              8 
        MEXICO      NICARAGUA         PANAMA  UNITED STATES      ARGENTINA 
             8              8              8              9              9 
       BOLIVIA         BRAZIL          CHILE       COLOMBIA        ECUADOR 
             1              6             10              8              6 
          PERU        URUGUAY      VENEZUELA        AUSTRIA        BElGIUM 
             5              9              8              2              2 
       BRITAIN       BULGARIA CZECHOSLOVAKIA        DENMARK        FINLAND 
             2              7              7              4              2 
     E.GERMANY      W.GERMANY         GREECE        HUNGARY        IRELAND 
             2              2              1              7              9 
         ITALY    NETHERLANDS         NORWAY         POLAND       PORTUGAL 
             2              9              2              1              9 
       ROMANIA          SPAIN         SWEDEN    SWITZERLAND       U.S.S.R. 
             7              9              7              2              9 
    YUGOSLAVIA      AUSTRALIA    NEW ZEALAND 
             9              9              5 

Within cluster sum of squares by cluster:
 [1]  18.08800  24.76444  28.17000   0.00000  45.19429  69.57429  22.67667
 [8]  97.49778  24.53636 123.05455
 (between_SS / total_SS =  95.8 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"    
[5] "tot.withinss" "betweenss"    "size"         "iter"        
[9] "ifault"

如上结果中显示了10个类别数所含的样本数、各类别中心点坐标、聚类向量（各个国家地区具体属于哪个类别）、以及聚类优度，即组间平方和占总平方和的95.8%，该值可用于与类别数取不同值时的聚类结果进行比较，从而找出最优聚类结果，该百分数越大表明组内差距越小、组间差距越大，即聚类效果越好。
最后简单查看k=10时，与中国大陆属于同一类别的国家和地区有哪些：

> cluster_CHINA = fit_km1$cluster[which(countries$country == 'CHINA')]
> which(fit_km1$cluster == cluster_CHINA)
   ALGERIA      CONGO     CEYLON      CHINA     TAIWAN  HONG KONG   MALAYSIA 
         1          2         10         11         12         13         20 
  MONGOLIA   THAILAND DOMINICANR      CHILE 
        21         24         28         38

2.2 K-中心点聚类

与K-均值算法在原理上十分相近，针对于K-均值算法易受极值影响这一缺点进行改进。原理上的差异在于选择各类别中心点时不取样本均值点，而在类别内选取到其余样本距离之和最小的样本为中心。
调用Cluster包的pam()函数实现：pam(x, k, diss = inherits(x, "dist") , metric = "euclidean" , medoids = NULL, stand = FALSE, cluster.only = FALSE, do.swap = TRUE , keep.diss = !diss && !cluster.only && n<l00 , keep.data = !diss && ! cluster.only，pamonce = FALSE , trace.lev = 0)

接着上面的案例，看看用K-中心点聚类输出的结果有何不同：

> library(cluster)
> fit_pam = pam(countries[, -1], 10)
> print(fit_pam)
Medoids:
            ID birth death
MALAGASY     6  41.8  15.8
THAILAND    24  34.8   7.9
IVORY COAST  5  56.1  33.1
MOROCCO      7  46.1  18.7
COLOMBIA    39  44.0  11.7
AUSTRALIA   67  21.6   8.7
PERU        41  27.7   8.2
BULGARIA    47  16.4   8.2
NICARAGUA   32  42.9   7.1
BRITAIN     46  18.2  12.2
Clustering vector:
       ALGERIA          CONGO          EGYPT          GHANA    IVORY COAST 
             1              2              1              3              3 
     ……

    YUGOSLAVIA      AUSTRALIA    NEW ZEALAND 
             6              6              7 
Objective function:
   build     swap 
2.216542 2.134175 

Available components:
 [1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
 [6] "clusinfo"   "silinfo"    "diss"       "call"       "data"

在输出结果中，相对于kmeans()多出了中心点(Medoids)一项，该项指明了聚类完成时各类别的中心点分别是哪几个样本点，它们的变量取值为多少。此外，目标方程项(Objective function) 给出了build 和swap 两个过程中目标方程的值。其中，build过程用于在未指定初始中心点情况下，对于最优初始中心点的寻找；而swap过程则用于在初始中心点的基础上，对目标方程寻找使其能达到局部最优的类别划分状态，即其他划分方式都会使得目标方程的取值低于该值（老实说我不是很理解这个==）。

2.3 系谱聚类

相对于K-均值算法与K-中心点算法，系谱算法的突出特点在于，不需事先设定类别数k，这是因为它每次选代过程仅将距离最近的两个样本/簇聚为一类，其运作过程将自然得到k=1至k=n(n为待分类样本总数)个类别的聚类结果。
调用stats包的hclust()、cutree()、rect.hclust()函数实现：hclust(d, method = "complete", members = NULL)
cutree()函数则可以对hclust()函数的聚类结果进行剪枝，即选择输出指定类别数的系谱聚
类结果。其格式为：cutree(tree, k = NULL, h = NULL)
函数rect.Bclust()可以在plot()形成的系谱图中将指定类别中的样本分支用方框表示出来，十分有助于直观分析聚类结果。其基本格式为：rect.hclust(tree, k = NULL, which = NULL, X = NULL, h = NULL, border = 2, cluster = NULL)

对该案例进行系谱聚类，首先使用dist()函数中默认的欧式距离来生成Countries数据集的距离矩阵，再使用hclust()函数展开系谱聚类，并生成系谱图：

> fit_hc = hclust(dist(countries[, -1]))
> print(fit_hc)

Call:
hclust(d = dist(countries[, -1]))

Cluster method   : complete 
Distance         : euclidean 
Number of objects: 68 
> plot(fit_hc)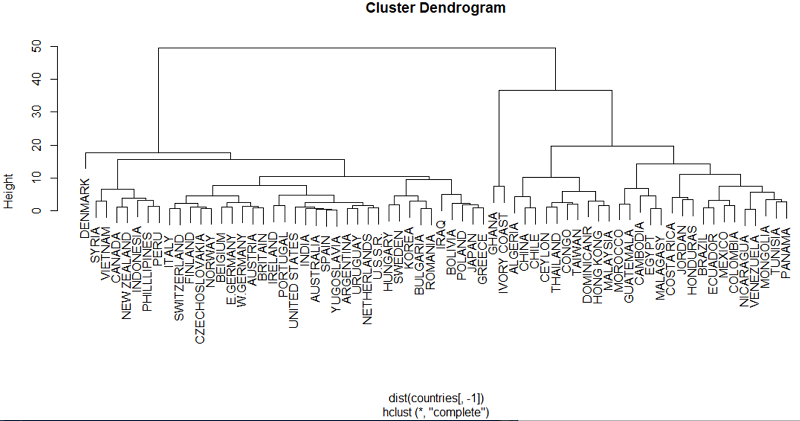

从系谱图可以看出，在图的最下端每个国家各占一个分支自成一类，越往上看，一条分支下的国家数越多，直至最上端所有国家聚为一类。在图的左侧以高度指标(Height)衡量树形图的高度，这一指标在下面将要提到的剪枝过程中将会用到。
接下来利用剪枝函数cutree()中的参数k和参数h分别控制输出10类别和Height=15时的系谱聚类结果：

#利用剪枝函数cutree()中的参数k控制输出10类别的系谱聚类结果
> group_k10 = cutree(fit_hc, k = 10)
> group_k10
       ALGERIA          CONGO          EGYPT          GHANA    IVORY COAST 
             1              2              3              4              4 
     ……

    YUGOSLAVIA      AUSTRALIA    NEW ZEALAND 
             6              6              7 
> table(group_k10)
group_k10
 1  2  3  4  5  6  7  8  9 10 
 3  7  5  2  9 21  7 10  3  1 
#查看如上k=10的聚类结果中各类别样本
> sapply(unique(group_k10), function(g)countries$country[group_k10 == g])
[[1]]
[1] ALGERIA CHINA   CHILE  
68 Levels: ALGERIA ARGENTINA AUSTRALIA AUSTRIA BElGIUM BOLIVIA ... YUGOSLAVIA

……

[[10]]
[1] DENMARK
68 Levels: ALGERIA ARGENTINA AUSTRALIA AUSTRIA BElGIUM BOLIVIA ... YUGOSLAVIA

#利用剪枝函数cutree()中的参数h控制输出Height=15时的系谱聚类结果
> group_h15 = cutree(fit_hc, h = 15)
> table(group_h15)
group_h15
 1  2  3  4  5  6 
10 17  2 31  7  1

最后使用rect.hclus()函数从系谱图中选择查看聚类结果:

1
2
3

> plot(fit_hc)
> rect.hclust(fit_hc, k = 4, border = 'blue')
> rect.hclust(fit_hc, k = 7, border = 'red')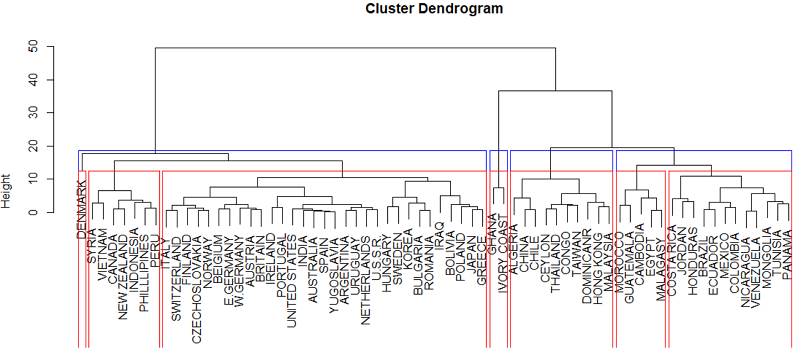

图中蓝色方框为4分类的结果，红色方框为7分类的结果。此图清晰地呈现了7类别是在原有的4类别的第一分类和第四分类的基础上进行再分类形成的。

2.4 密度聚类

基于密度的聚类算法相对于如上算法，其优势在于弥补了它们只能发现”类圆形”聚类簇的缺陷，该类算法由于是基于”密度”来聚类的，可以在具有噪声的空间数据库中发现任意形状的簇。DBSCAN叫算法是基于密度的聚类方法(Density-based Methods)中最常用的代表算法之一，具体算法可以参考Python部分笔记。
调用fpc包的dbscan()函数实现：dbscan (data, eps, Minpts = 5, scale = FALSE, method = c ("hybrid", "raw", "dist ") , seeds = TRUE, showplot = FALSE, countmode = NULL)

dbscan算法将数据点分为三类：
-核心点：在半径eps内含有超过MinPts数目的点。
-边界点：在半径eps内点的数量小于MinPts，但是落在核心点的邻域内的点。
-噪音点：既不是核心点也不是边界点的点。

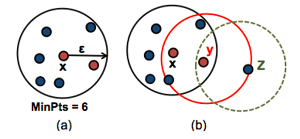
如上图(a)，数据集中任意点x邻居(MinPts=6)都被标记为核心点，eps为半径。图(b)中，x为核心点，y的邻居小于MinPts(4<6)，但它属于核心点x的最邻居，是边界点。z点既不是核心也不是边界点，它被称为噪声点或异常值。

针对该案例，首先查看大多数样本间的距离是在怎样一个范围，再以此距离作为半径参数的取值：

> library(fpc)
> d = dist(countries[, -1])
> max(d);min(d)
[1] 49.56259
[1] 0.2236068
#加载ggplot2软件包，使用数据分段函数cut_interval()函数对各样本间的距离进行分段处理
> library(ggplot2)
#结合最大位最小值相差50左右，取居中段数为30
> interval = cut_interval(d, 30)
> table(interval)
interval
[0.224,1.87]  (1.87,3.51]  (3.51,5.16]   (5.16,6.8]   (6.8,8.45] 
          78          156          222          201          151 
 (8.45,10.1]  (10.1,11.7]  (11.7,13.4]    (13.4,15]    (15,16.7] 
         121          141          100           93          104 
 (16.7,18.3]    (18.3,20]    (20,21.6]  (21.6,23.2]  (23.2,24.9] 
         104           89          101           97          101 
 (24.9,26.5]  (26.5,28.2]  (28.2,29.8]  (29.8,31.5]  (31.5,33.1] 
         100           83           75           38           30 
 (33.1,34.8]  (34.8,36.4]  (36.4,38.1]  (38.1,39.7]  (39.7,41.3] 
          12            8            8           12           11 
   (41.3,43]    (43,44.6]  (44.6,46.3]  (46.3,47.9]  (47.9,49.6] 
          14           13            8            5            2 
#找出所含样本点最多的区间
> which.max(table(interval))
(3.51,5.16] 
          3 
#对半径取3、4、5，密度阈值为1至10，作双层循环
> for (i in 3:5) {
+     for (j in 1:10) {
+         ds = dbscan(countries[, -1], eps = i, MinPts = j)
+         print(ds)
+     }
+ }
dbscan Pts=68 MinPts=1 eps=3
      1  2 3 4 5 6  7 8 9 10 11
seed  1 21 1 1 2 1 37 1 1  1  1
total 1 21 1 1 2 1 37 1 1  1  1
……
dbscan Pts=68 MinPts=9 eps=5
       0  1  2
border 6 16  3
seed   0  9 34
total  6 25 37
dbscan Pts=68 MinPts=10 eps=5
       0  1  2
border 7 18  4
seed   0  6 33
total  7 24 37

以上结果中，seed所对应的行表示的是相互密度可达的核心点，border所对应的行表示的是边缘点，0所对应列为噪音点的个数，列数1、2、3表示聚类结果的类别数，如最后一个结果总共聚类为2类，两类的样本个数(包含核心点和边界点)分别为24和37，噪音点个数为7。

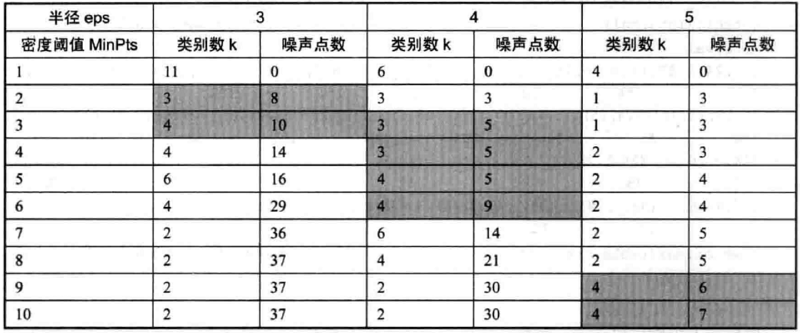
将30次的聚类结果整理汇总如上表，选择合适的参数值。一般来说，类别数应至少高于2类，否则进行聚类的意义不大；并且噪声点不应太多，若太多则说明参数条件过紧，参与有效聚类的样本点太少。符合条件的为阴影部分的取值。
选取其中三组参数(eps=3，MinPts=2；eps=4，MinPts=5；eps=5，MinPts=9)所对应的聚类结果进行绘图：

> ds5 = dbscan(countries[, -1], eps = 3, MinPts = 2)
> ds6 = dbscan(countries[, -1], eps = 4, MinPts = 5)
> ds7 = dbscan(countries[, -1], eps = 5, MinPts = 9)
> par(mfcol = c(1, 3))
> plot(ds5, countries[, -1], main = '5: MinPts=2 eps=3')
> plot(ds6, countries[, -1], main = '6: MinPts=5 eps=4')
> plot(ds7, countries[, -1], main = '7: MinPts=9 eps=5')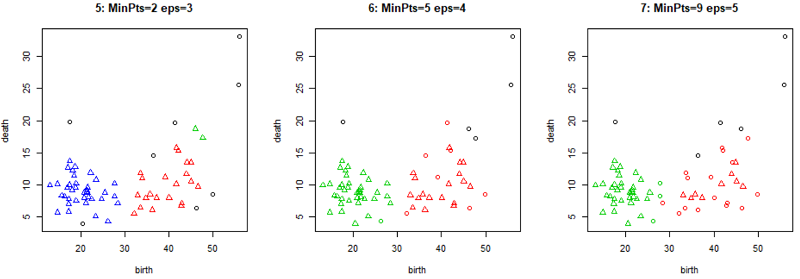

由以上过程，总结出DBSCAN算法参数取值的规律: 半径参数与阈值参数的取值差距越大，所得类别总数越小；半径参数相对于阈值参数较小时，越多的样本被判定为噪音点(这个规律其实不是特别准…)

2.5 期望最大化聚类

在使用该算法进行聚类时，它将数据集看作一个含有隐性变量的概率模型，并以实现模型最优化，即获取与数据本身性质最契合的聚类方式为目的，通过”反复估计”模型参数找出最优解，同时给出相应的最优类别数k。而”反复估计”的过程即是EM 算法的精华所在，这一过程由E-step (Expectation)和M-step(Maximization) 这两个步骤交替进行来实现。

调用mclust包的Mclust()、mclustBIC()、mclust2Dplot()、densityMclust()函数实现：Mclust(data, G = NULL, modelNames = NULL, prior = NULL, control = emControl(), initialization = NULL, warn = FALSE, ... )
mclustBIC()函数的参数设置与Mclust()基本一致，用于获取数据集所对应的参数化高斯混合模型的BIC值，而BIC值的作用即是评价模型的优劣，BIC值越高模型越优。mclust2Dplot()可根据EM算法所生成参数对二维数据制图。densityMclust()函数利用Mclust()的聚类结果对数据集中的每个样本点进行密度估计。

用Mclust()函数直接对数据进行期望最大化聚类：

> library(mclust)
> fit_EM = Mclust(countries[, -1])
> summary(fit_EM)
---------------------------------------------------- 
Gaussian finite mixture model fitted by EM algorithm 
---------------------------------------------------- 

Mclust EII (spherical, equal volume) model with 4 components: 

 log-likelihood  n df      BIC       ICL
       -418.415 68 12 -887.464 -893.5937

Clustering table:
 1  2  3  4 
 2 13 17 36

以上结果显示，根据BIC选择出的最佳模型类型为EII，最优类别数为4，各类别分别含有2、13、17、36个样本。
对Mclust的聚类结果直接绘图：

> plot(fit_EM)
Model-based clustering plots: 

1: BIC
2: classification
3: uncertainty
4: density

得到4张图形，分别为BIC图、分类图(classification)、概率图(uncertainty)以及密度图(density)。

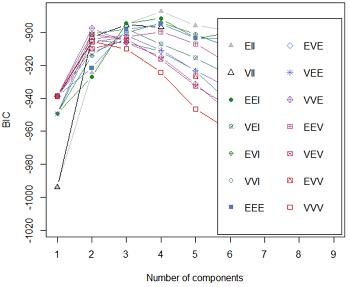
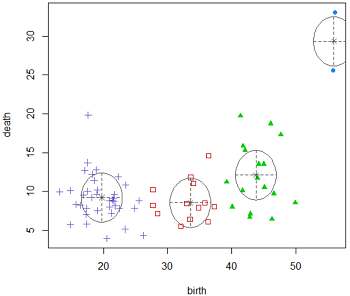
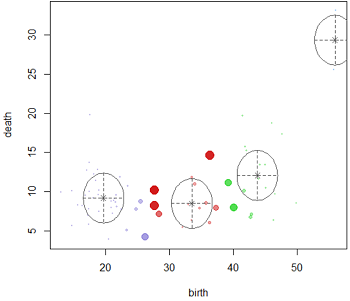
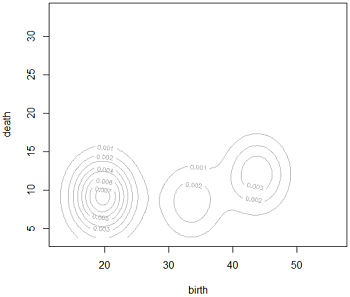
比如概率图不仅将各类别样本的主要分布区域用椭圆圈出，并标出了类别中心点，且以样本点图形的大小来显示该样本归属相应类别的概率大小。
下面用mclustBIC()函数来试试其他结果：

> countries_BIC = mclustBIC(countries[, -1])
> countries_BICsum = summary(countries_BIC, data = countries[, -1])
> countries_BICsum
Best BIC values:
            EII,4       EEI,4       EVI,4
BIC      -887.464 -891.670811 -894.177259
BIC diff    0.000   -4.206773   -6.713222

Classification table for model (EII,4): 

 1  2  3  4 
 2 13 17 36

得到的结果都是4分类的EII、EEI和EVI模型，其中EII模型的结果与Mclust()得到的结果一致。
也可以进一步对该结果进行绘图，这里就不放上来了。

3 思考

5种聚类算法内容很丰富，但是除了会调用软件包和使用函数，其实对有些算法的具体实现过程还是比较模糊的，希望以后有机会接触进一步学习。
这里也有个疑问：为什么同一批数据集，用k-means聚类得到是分为10类比较好，而用密度聚类和期望最大化聚类则是分为3或4类呢？以及如何评估聚类结果的好坏呢？

本笔记基于黄文和王正林编著的《数据挖掘：R语言实战》整理