关联分析用于从大量数据中发现项集之间的有趣关联或相互关系,最经典的是Apriori 算法。
1 基本概念
(1)项集:项目的集合,一个项集包含K项,则称之为K元项集。如{啤酒,尿布}构成一个二元项集。
(2)关联规则:一般记为 X → Y 的形式,称关联规则左侧的项集X为先决条件(lhs),右侧项集Y为相应的关联结果(rhs),用于表示出数据内隐含的关联性。
(3)关联性的强度
支持度:是指在所有项集中{X , Y}出现的可能性,即项集中同时含有X和Y的概率。通过设定最小阈值,支持度大于等于最小阈值的成为频繁项集。Support(X → Y) = P(X, Y)
置信度:表示在关联规则的先决条件X发生的条件下,关联结果Y发生的概率,即含有X的项集中,同时含有Y 的可能性。Confidence(X → Y) = P(Y | X) = P(X, Y) / P(X)
提升度:表示在含有X的条件下同时含有Y的可能性与没有这个条件下项集中含有Y的可能性之比,即在Y自身出现可能性P(Y)的基础上, X的出现对于Y的”出镜率” P(Y|X)的提升程度。Lift(X → Y) = P(Y | X) / P(Y) = Confidence(X → Y) / P(Y)
当lift值为1时表示X与Y相互独立,X对Y出现的可能性没有提升作用,而其值越大(>1)则表明X对Y的提升程度越大,也即表明关联性越强。
下面举个栗子来简单理解一下这三个“度”:
假设有10000个消费者购买商品,其中购买尿布的有1000个,购买啤酒的有2000个,购买面包的有500个,且同时购买尿布与啤酒的有800个,同时购买尿布与面包的有100个。
支持度:设定支持度的最小阈值为5%,S{尿布,啤酒}=800/10000=8%,S{尿布,面包}=100/10000=1%。所以{尿布,啤酒}成为频繁项集,且两条规则尿布 → 啤酒、啤酒 → 尿布同时被保留,而{尿布,面包}所对应的两条规则被排除。
置信度:设定置信度的最小阈值为70%,P(尿布)=1000/10000=10%,P(啤酒)=2000/10000=20%,C(尿布→啤酒)=8%/10%=80%,C(啤酒→尿布)=8%/20%=40%。所以,根据最小阈值筛选出一条强关联规则:尿布→啤酒。
提升度:L(尿布→啤酒)=80%/20%=4,这表明尿布对啤酒的出现的可能性具有很大的提升作用。
2 算法的基本步骤
(1)选出满足支持度最小阈值的所有项集,即频繁项集。该阈值一般设定为5%~ 10%。
(2)从频繁项集中找出满足最小置信度的所有规则。置信度的阈值往往设定得较高,如70%~90%。
3 在R中的实现
R 中有两个专用于关联分析的软件包——arules和arulesViz,。其中,arules 用于关联规则的数字化生成,提供Apriori 和Eclat 这两种快速挖掘频繁项集和关联规则算法的实现函数;而arulesViz 软件包作为arules 的扩展包,提供了儿种实用而新颖的关联规则可视化技术,使得关联分析从算法运行到结果呈现一体化。
apriori 函数:apriori(data , parameter = NULL, appearance = NULL, control = NULL)
eclat 函数:eclat(data, parameter=NULL, control=NULL)
3.1 数据集准备
选用arules包自带的数据集Groceries,该数据集是某一食品杂货店一个月的真实交易数据。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36> library(arules)
> data("Groceries")
> inspect(Groceries[1:5]) #通过inspect函数查看Groceries数据集的前5条交易记录
items
[1] {citrus fruit,semi-finished bread,margarine,ready soups}
[2] {tropical fruit,yogurt,coffee}
[3] {whole milk}
[4] {pip fruit,yogurt,cream cheese ,meat spreads}
[5] {other vegetables,whole milk,condensed milk,long life bakery product}
> summary(Groceries)
transactions as itemMatrix in sparse format with
9835 rows (elements/itemsets/transactions) and
169 columns (items) and a density of 0.02609146
most frequent items:
whole milk other vegetables rolls/buns soda
2513 1903 1809 1715
yogurt (Other)
1372 34055
element (itemset/transaction) length distribution:
sizes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2159 1643 1299 1005 855 645 545 438 350 246 182 117 78 77 55
16 17 18 19 20 21 22 23 24 26 27 28 29 32
46 29 14 14 9 11 4 6 1 1 1 1 3 1
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 2.000 3.000 4.409 6.000 32.000
includes extended item information - examples:
labels level2 level1
1 frankfurter sausage meat and sausage
2 sausage sausage meat and sausage
3 liver loaf sausage meat and sausage
由结果我们可以获得Groceries的基本信息,它包含9835条交易以及169个项,即商品;全脂牛奶(whole milk)是最受欢迎的商品,之后为蔬菜(other vegetables)、面包卷(rolls/buns)等。
3.2 模型初探
首先尝试对apriori()函数以最少的限制,来观察它可以反馈给我们哪些信息,再以此决定下一步操作。这里将支持度的最小阈值设置为0.001,置信度最小阈值设为0.5,其他参数不进行设定取默认值:1
2
3
4
5
6
7
8
9
10> rules0 = apriori(Groceries, parameter = list(support = 0.001, confidence = 0.5))
> rules0
set of 5668 rules
> inspect(rules0[1:5])
lhs rhs support confidence lift count
[1] {honey} => {whole milk} 0.001118454 0.7333333 2.870009 11
[2] {tidbits} => {rolls/buns} 0.001220132 0.5217391 2.836542 12
[3] {cocoa drinks} => {whole milk} 0.001321810 0.5909091 2.312611 13
[4] {pudding powder} => {whole milk} 0.001321810 0.5652174 2.212062 13
[5] {cooking chocolate} => {whole milk} 0.001321810 0.5200000 2.035097 13
这里对第一条规则解读一下:如果一个顾客购买了蜂蜜(honey),那么他还会购买全脂牛奶(whole milk),支持度为0.0011,置信度为0.7333,这表示该规则涵盖了大约0.1%的交易,而且在购买了蜂蜜后,他购买全脂牛奶的概率为73.3%,提升度为2.87,表明(购买蜂蜜之后再购买全脂牛奶的可能性)是(没有购买蜂蜜但是购买全脂牛奶的可能性)的2.87倍,即相对于一般没有购买蜂蜜的顾客购买全脂牛奶的概率提升了2.87倍。
该结果显示有5668条关联规则,如此大量的关联规则全部输出是没有意义的,而且信息的排序没有规则可言。因此,接下来要考虑选择其中关联性较强的若干条规则。
3.3 对生成规则进行强度控制
最常用的方法是通过提高支持度和/或置信度的值来实现,这往往是一个不断调整的过程。如果阈值设定过高,容易丢失有用信息,如果过低,则生成大量规则信息。最终关联规则的规模大小是根据使用者的需求决定的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18#通过支持度、置信度共同控制
> rules1 = apriori(Groceries, parameter = list(support = 0.005, confidence = 0.5))
> rules1
set of 120 rules
> rules2 = apriori(Groceries, parameter = list(support = 0.005, confidence = 0.60))
> rules2
set of 22 rules
> rules3 = apriori(Groceries, parameter = list(support = 0.005, confidence = 0.64))
> rules3
set of 4 rules
#通过对“三度”进行单独控制
> inspect(sort(rules2, by = 'support')[1:2])
lhs rhs support confidence lift count
[1] {butter,yogurt} => {whole milk} 0.009354347 0.6388889 2.500387 92
[2] {root vegetables,butter} => {whole milk} 0.008235892 0.6377953 2.496107 81
#同理,对置信度和提升度的控制可以通过by参数设置
3.4 改变结果的输出形式
apriori()和eclat()函数都可以根据需要输出频繁项集(frequent itemsets)等其他形式结果。
比如当我们想知道某超市这个月销售量最高的商品,可以将apriori()中目标参数设置为”frequent itemsets”:1
2
3
4
5
6
7
8
9
10> itemsets_apr = apriori(Groceries, parameter = list(supp = 0.001, target = 'frequent itemsets'), control = list(sort = -1))
> itemsets_apr
set of 13492 itemsets
> inspect(itemsets_apr[1:5])
items support count
[1] {whole milk} 0.2555160 2513
[2] {other vegetables} 0.1934926 1903
[3] {rolls/buns} 0.1839349 1809
[4] {soda} 0.1743772 1715
[5] {yogurt} 0.1395018 1372
如上结果显示将sort参数对项集频率进行降序排序后,销量前5的商品分别为全脂牛奶、蔬菜、面包卷、苏打以及酸奶。
以下我们使用eclat()函数来取最适合进行捆绑销售,或者说相近摆放的5对商品:1
2
3
4
5
6
7
8
9
10> itemsets_ecl = eclat(Groceries, parameter = list(minlen = 1, maxlen = 3, supp = 0.001, target = 'frequent itemsets'), control = list(sort = -1))
> itemsets_ecl
set of 9969 itemsets
> inspect(itemsets_ecl[1:5])
items support count
[1] {whole milk,honey} 0.001118454 11
[2] {whole milk,cocoa drinks} 0.001321810 13
[3] {whole milk,pudding powder} 0.001321810 13
[4] {tidbits,rolls/buns} 0.001220132 12
[5] {tidbits,soda} 0.001016777 10
输出结果中的全脂牛奶和蜂蜜,以及全脂牛奶与苏打作为共同出现最为频繁的两种商品,则可以考虑采取相邻摆放等营销策略。
这里注意:在iternsets的生成代码中,并没有对confidence值进行设置,这里并非选择了取默认值,而是因为频繁项集的产生仅与支持度阈值有关。
另外,如果我们想促销一种比较冷门的商品——芥末(mustard),可以通过将函数apriori()中的关联结果(rhs) 参数设置为”mustard”,来搜索出rhs中仅包含mustard 的关联规则,从而有效地找到mustard的强关联商品,来作为捆绑商品。另外,还设置参数maxlen为2,控制lhs中仅包含一种食品,因为实际上我们仅将两种商品进行捆绑,而不是一堆商品:1
2
3
4> rules4 = apriori(Groceries, parameter = list(maxlen = 2, supp = 0.001, conf = 0.1), appearance = list(rhs = 'mustard', default = 'lhs'))
> inspect(rules4)
lhs rhs support confidence lift count
[1] {mayonnaise} => {mustard} 0.001423488 0.1555556 12.96516 14
3.5 关联规则的可视化
关联规则的可视化需要用到arulesViz软件包:1
2
3
4
5
6
7
8
9
10
11
12
13
14> library(arulesViz)
> rules5 = apriori(Groceries, parameter = list(support = 0.002, confidence = 0.5))
> rules5
set of 1098 rules
> plot(rules5) #见左图
#可以通过更改参数设置,来变换横纵轴及颜色条所对应的变量,图略
> plot(rules5, measure = c('support', 'lift'), shading = 'confidence')
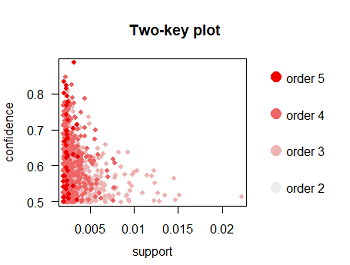
#将shading参数设置为"order"来绘制出一种特殊的散点图——Two-key散点图,见右图
> plot(rules5, shading = 'order', control = list(main = 'Two-key plot'))
#将图形类型更改为"grouped"生成分组图,见底图
> plot(rules5, method = 'grouped')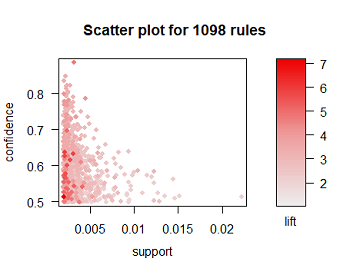
左图图中每个点对应于相应的支持度和置信度值,且其中关联规则点的颜色深浅由lift值的高低决定。可以看出大量规则的参数取值分布情况,如提升度较高的关联规则的支持度往往较低,支持度与置信度具有相反相关性等。如果想具体的值这些规则对应的是哪些商品及关联强度如何等信息,可以通过设置互动参数(interactive)来进行交互显示(这里就不放上来啦)。
右图散点图的横纵轴依然为支持度和置信度,而关联规则点的颜色深洗则表示其所代表的关联规则中含有商品的多少, 商品种类越多,点的颜色越深。
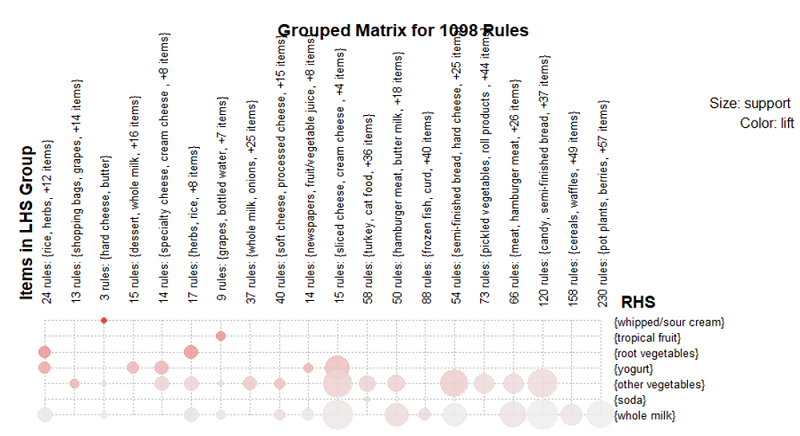
图中按照lift参数来看, 关联性最强(圆点颜色最深)的两种商品为{hard cheese, butter}与{whipped/sour cream}; 而以support参数来看则是{candy, semi-finished bread}与{whole milk}关联性最强(圆点尺寸最大〉。
- 本笔记基于黄文和王正林编著的《数据挖掘:R语言实战》整理

