Kmeans聚类算法有两个缺点,一是聚类效果容易受到异常样本点的影响,二是该算法无法准确地将非球形样本进行合理的聚类,而基于密度的聚类DBSCAN(Density-Based Special Clustering of Applications with Noise)可以弥补这两个缺点。“密度”可以理解为样本点的紧密程度,而紧密度的衡量需要使用半径和最小样本量进行评估,如果在指定的半径领域内,实际样本量超过给定的最小样本量阈值,则认为是密度高的对象。该算法可以非常方便地发现样本集中的异常点,故可以通常使用该算法实现异常点的检测。
另外,层次聚类算法则比较适合小样本的聚类,它是通过计算各个簇内样本点之间的相似度,进而构建一棵有层次的嵌套聚类树。该算法仍然不适合非球形样本的聚类,但它与Kmeans算法类似,可以通过人为设定聚类个数实现样本点的聚合,相比于密度聚类算法来说,似乎方便很多。
1 密度聚类
1.1 密度聚类的步骤
密度聚类的过程有点像贪吃蛇,从某个点出发,不断地向外扩张,直到获得一个最大的密度相连,进而形成一个样本簇。具体步骤如下:
1)为密度聚类算法设置一个合理的半径以及该半径领域所包含的最少样本量。
2)从数据集中随机挑选一个样本点p,检验其在半径领域内是否包含指定的最少样本量,如果包含就将其定为核心对象,并构成一个簇C;否则,重新挑选一个样本点。
3)对于核心对象p所覆盖的其他样本点q,如果点q对应的半径领域内仍然包含最少样本量,就将其覆盖的样本点统统归于簇C。
4)重复步骤3,将最大的密度相连所包含的样本点聚为一类,形成一个大簇。
5)完成步骤4后,重新回到步骤2,并重复步骤3和4,直到没有新的样本点可以生成新簇时,算法结束。
密度算法可以通过调用sklearn子模块cluster中的DBSCAN类实现。
1.2 密度聚类与Kmeans的比较
球形簇样本点
首先通过随机抽样的方法形成两个球形簇的样本集,然后对比密度聚类和Kmeans聚类算法的聚类结构。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
#模拟数据集
X, y = make_blobs(n_samples=2000, centers = [[-1, -2], [1, 3]],
cluster_std=[0.5, 0.5], random_state=1234)
#将数组转换为数据框用于绘图
plot_data = pd.DataFrame(np.column_stack((X, y)), columns = ['x1', 'x2', 'y'])
#绘制散点图
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y', markers = ['^', 'o'],
fit_reg=False, legend=False, scatter_kws={'color': 'steelblue'})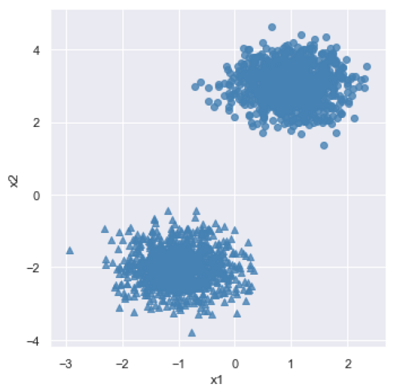
接下来用密度聚类和Kmeans聚类两种方法对上面的样本集进行聚类:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17from sklearn import cluster
kmeans = cluster.KMeans(n_clusters=2, random_state=1234)
kmeans.fit(X)
dbscan = cluster.DBSCAN(eps = 0.5, min_samples=10)
dbscan.fit(X)
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_
plt.figure(figsize = (12, 6))
#第一个子图绘制Kmeans聚类效果
ax1 = plt.subplot2grid(shape = (1, 2), loc = (0, 0))
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
#第二个子图绘制密度聚类效果
ax2 = plt.subplot2grid(shape = (1, 2), loc = (0, 1))
ax2.scatter(plot_data.x1, plot_data.x2,
c = plot_data.dbscan_label.map({-1: 1, 0: 2, 1: 0}))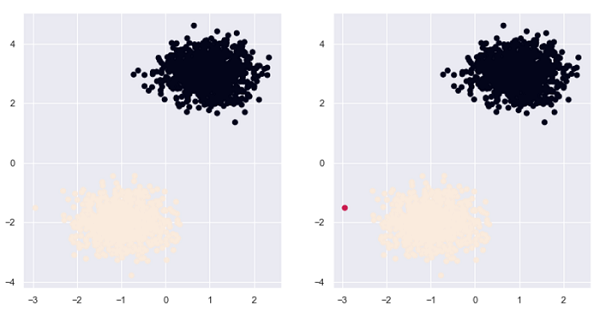
如图所示,两种算法在球形簇的样本点的效果都比较好,但是密度聚类发现了一个异常点,该点不属于任何一个簇。由此看出密度聚类算法可以发现远离簇的异常点。
非球形簇样本点
接下来看看两者在非球形簇的样本点的表现如何:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16from sklearn.datasets.samples_generator import make_moons
#构造非球形样本点
X1, y1 = make_moons(n_samples=2000, noise = 0.05, random_state=1234)
#构造球形样本点
X2, y2 = make_blobs(n_samples=1000, centers = [[3, 3]],
cluster_std=0.5, random_state=1234)
#位避免与y1值的冲突,将y2的值替换为2
y2 = np.where(y2 == 0, 2, 0)
#将数组转换数据框
plot_data = pd.DataFrame(np.row_stack([np.column_stack((X1, y1)),
np.column_stack((X2, y2))]),
columns = ['x1', 'x2', 'y'])
#画图
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y', markers = ['^', 'o', '>'],
fit_reg=False, legend=False)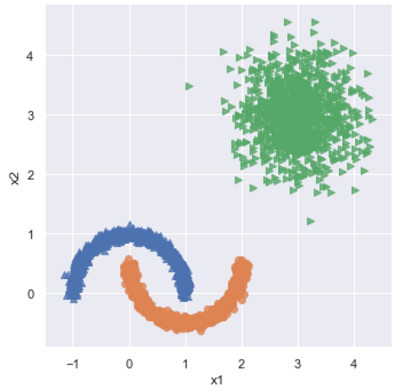
如图生成了三个簇的样本点,左下角代表两个非球形簇。下面用两种算法就行聚类:1
2
3
4
5
6
7
8
9
10
11
12
13kmeans = cluster.KMeans(n_clusters=3, random_state=1234)
kmeans.fit(plot_data[['x1', 'x2']])
dbscan = cluster.DBSCAN(eps = 0.3, min_samples=5)
dbscan.fit(plot_data[['x1', 'x2']])
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_
plt.figure(figsize = (12, 6))
ax1 = plt.subplot2grid(shape = (1, 2), loc = (0, 0))
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
ax2 = plt.subplot2grid(shape = (1, 2), loc = (0, 1))
ax2.scatter(plot_data.x1, plot_data.x2,
c = plot_data.dbscan_label.map({-1: 2, 0:0, 1: 3, 2: 1}))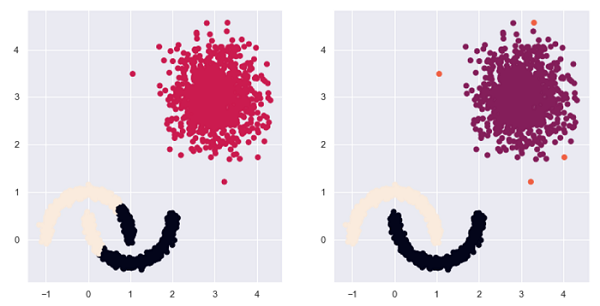
如图所示,密度聚类不仅将异常点也检验出来,而且也将非球形簇准确地划分出来(右图)。
2 层次聚类
层次聚类的实质是计算各簇内样本点之间的相似度,并通过相似度的结果构建凝聚或分裂的层次树。不管是凝聚还是分裂过程,都需要回答两个问题,一是样本点之间通过什么指标衡量它们之间的相似性,这与Kmeans类似,可以通过欧氏距离或曼哈顿距离来衡量,距离越近,相似性越高;二是如何衡量簇与簇之间的聚类,有三种方法:最小距离法、最大距离法和平均距离法。
该算法可以通过调用sklearn子模块cluster的AgglomerativeClustering类实现。
2.1 层次聚类的步骤
层次聚类的步骤如下:
1)将数据集中的每个样本点当做一个类别;
2)计算所有样本点之间的两两距离,并从中挑选出最小距离的两个点构成一个簇;
3)继续计算剩余样本点之前的两两距离和点与簇之间的距离,然后将最小距离的点或簇合并到一起;
4)重复步骤2和3,直到满足聚类的个数或其他设定的条件,算法结束。
2.2 三种层次聚类的比较
层次聚类对球形簇的样本点会有比较好的聚类效果,接下来随机生成两个球形簇的样本点,利用层次聚类算法进行聚类,比较三种簇间的距离指标所形成的聚类差异。1
2
3
4
5X, y = make_blobs(n_samples=2000, centers = [[-1, 0], [1, 0.5]],
cluster_std=[0.2, 0.45], random_state=1234)
plot_data = pd.DataFrame(np.column_stack((X, y)), columns = ['x1', 'x2', 'y'])
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',
markers = ['<', 'o'], fit_reg = False, legend = False)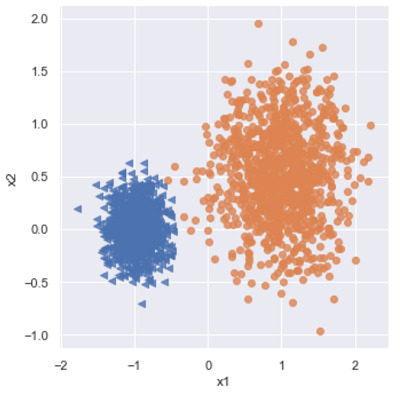
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18plt.figure(figsize = (16, 5))
#层次聚类:最小距离法
ax1 = plt.subplot2grid(shape = (1, 3), loc = (0, 0))
agnes_min = cluster.AgglomerativeClustering(n_clusters=2, linkage='ward')
agnes_min.fit(X)
ax1.scatter(X[:, 0], X[:, 1], c = agnes_min.labels_)
#最大距离法
ax2 = plt.subplot2grid(shape = (1, 3), loc = (0, 1))
agnes_max = cluster.AgglomerativeClustering(n_clusters=2, linkage = 'complete')
agnes_max.fit(X)
ax2.scatter(X[:, 0], X[:, 1], c = agnes_max.labels_)
#平均距离法
ax3 = plt.subplot2grid(shape = (1, 3), loc = (0, 2))
agnes_avg = cluster.AgglomerativeClustering(n_clusters=2, linkage = 'average')
agnes_avg.fit(X)
plt.scatter(X[:, 0], X[:, 1], c = agnes_avg.labels_)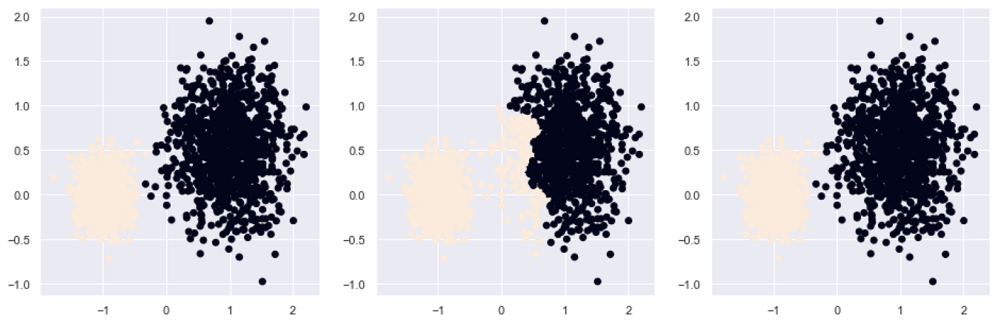
上图从左到右分别是最小距离法、最大距离法和平均距离法构成的聚类效果,由图中可以看出,最小距离法和平均距离法的聚类效果完全一样,并且相比于原始样本点,只有三个样本点被错误聚类,但最大距离法的聚类效果要差很多,主要是由于模糊地带(原始数据中两个簇交界的区域)的异常点夸大了簇之间的距离。
3 三种聚类的应用与对比
使用我国31个省的人口出生率和死亡率的数据,导入数据并绘制散点图:1
2
3
4
5province = pd.read_excel(r'C:\Users\Q\Desktop\Province.xlsx')
plt.scatter(province.Birth_Rate, province.Death_Rate)
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')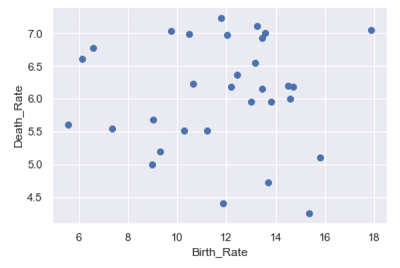
3.1 密度聚类
1 | from sklearn import preprocessing |
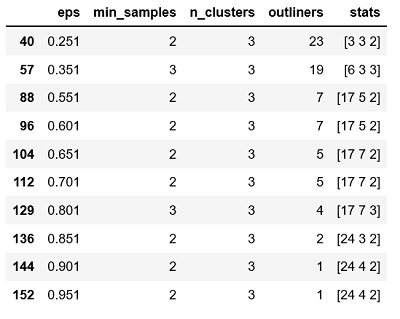
有两点需要注意:一是不管Kmeans聚类、密度聚类还是层次聚类,都有对用于聚类的原始数据做标准化处理;二是对密度聚类而言,通常需要不停地调试参数eps和min_samples,因为该算法的聚类效果在不同的参数组合下会有很大的差异。如果需要将数据聚为3类,可以得到以上结果,这里不妨选择eps为0.801、min_samples为3的参数值(因为参数组合下的异常点个数比较合理)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15dbscan = cluster.DBSCAN(eps = 0.801, min_samples = 3)
dbscan.fit(X)
province['dbscan_label'] = dbscan.labels_
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'dbscan_label',
data = province, markers = ['*', 'd', '^', 'o'],
fit_reg = False, legend = False)
for x, y, text in zip(province.Birth_Rate,province.Death_Rate,province.Province):
plt.text(x+0.1, y-0.1, text, size = 8)
plt.hlines(y = 5.8, xmin = province.Birth_Rate.min(),
xmax = province.Birth_Rate.max(), linestyle = '--', colors = 'red')
plt.vlines(x = 10, ymin = province.Death_Rate.min(),
ymax = province.Death_Rate.max(), linestyle = '--', colors = 'red')
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')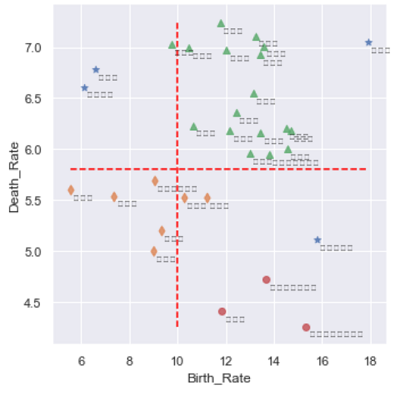
3.2 层次聚类
1 | #最小距离法构建层次聚类 |
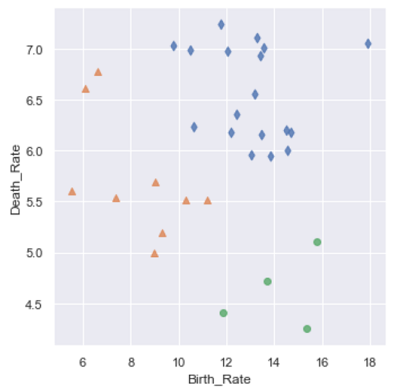
3.3 Kmeans聚类
1 | #用轮廓系数法构建kmeans聚类 |
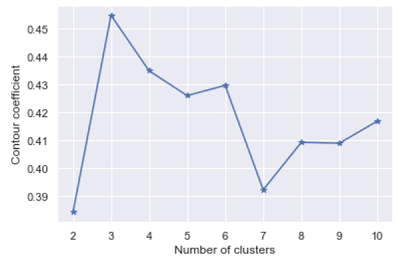
1
2
3
4
5
6
7
8kmeans = cluster.KMeans(n_clusters = 3)
kmeans.fit(X)
province['kmeans_label'] = kmeans.labels_
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'kmeans_label',
data = province, markers = ['d', '^', 'o'],
fit_reg = False, legend=False)
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')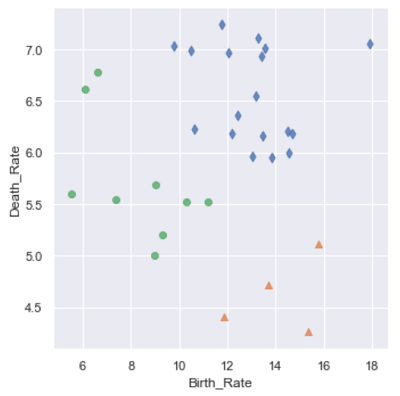
Kmeans聚类和层次聚类的效果完全一样。从上面的分析结果可知,该数据仍为球形分布的数据,因为三种聚类效果几乎一致,不同的是密度聚类可以非常方便地发现数据中的异常点。
- 本笔记基于刘顺祥的《从零开始学Python数据分析与挖掘》整理

