KNN,也叫K最近邻算法,它属于“惰性”学习算法,即不会预先生成一个分类或预测模型用于新样本的预测,而是将模型的构建与未知数据的预测同时进行,其核心思想是比较已知y值的样本与未知y值样本的相似度,然后寻找最相似的k个样本用作未知样本的预测。
KNN既可以针对离散因变量做分类,又可以对连续因变量做预测。对离散型的因变量来说,是从k个最近的已知类别样本中挑选出频率最高的类别用于未知样本的判断;对于连续型的因变量来说,则是将k个最近的已知样本均值用作未知样本的预测。
如分类算法的具体步骤为:
-确定未知样本近邻的个数k值;
-根据某种度量样本间相似度的指标(如欧氏距离)将每一个未知类别样本的最近k个已知样本搜寻出来,形成一个个簇;
-对搜寻出来的已知样本进行投票,将各簇下类别最多的分类作用于未知样本点的预测。
最佳k值的选择:设置k近邻样本的投票权重,通常可将权重设置为距离的倒数;采用多重交叉验证,该方案目前比较流行。
相似度的度量方法:欧氏距离、曼哈顿距离、余弦相似度、杰卡德相似系数
近邻样本的搜寻方法:暴力搜寻法、KD树搜寻法、球树搜寻法
分类问题和预测问题可分别使用sklearn子模块neighbors中调用KNeighborsClassifier类和KNeighborsRegressor类。
1 分类问题的解决
首先导入常用的程序库和读取数据集:1
2
3
4
5
6
7
8%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
Knowledge = pd.read_excel(r'C:\Users\Q\Desktop\Knowledge.xlsx')
Knowledge.head()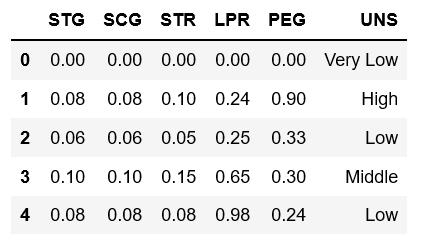
前5列分别为学生在目标学科上的学习时长(STG)、重复次数(SCG)、相关科目的学习时长(STR)、相关科目的考试成绩(LPR)和目标科目的考试成绩(PEG),5个指标均已做标准化处理;最后一列是学生对知识掌握程度的高低分类(UNS),有四种不同的值。
接下来拆分数据集和构造KNN分类模型:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn import neighbors
predictors = Knowledge.columns[:-1]
X_train, X_test, y_train, y_test = train_test_split(Knowledge[predictors],
Knowledge.UNS,
test_size = 0.25,
random_state = 1234)
#设置待测试的不同k值
K = np.arange(1, int(np.ceil(np.log2(Knowledge.shape[0]))))
#构建空列表存储平均准确率
accuracy = []
for k in K:
#使用10重交叉验证,比较每一个k值下KNN模型的预测准确率
cv_result = cross_val_score(neighbors.KNeighborsClassifier
(n_neighbors = k, weights = 'distance'),
X_train, y_train, cv = 10,
scoring = 'accuracy')
accuracy.append(cv_result.mean())
#从k个平均准确率中挑选出最大值对应的下标
arg_max = np.array(accuracy).argmax()
plt.scatter(K, accuracy)
plt.plot(K, accuracy)
plt.text(K[arg_max], accuracy[arg_max], 'the best k is %s' %int(K[arg_max]))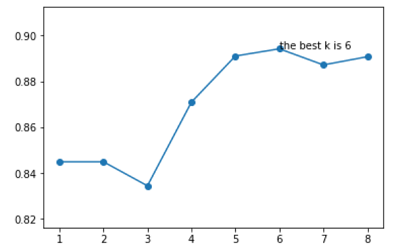
经过10重交叉验证,确定最佳的近邻个数为6个。
接下来利用这个最佳K值对训练集进行建模并绘制热力图:1
2
3
4
5
6
7
8knn_class = neighbors.KNeighborsClassifier(n_neighbors = 6, weights = 'distance')
knn_class.fit(X_train, y_train)
pred = knn_class.predict(X_test)
cm = pd.crosstab(pred, y_test)
#绘制热力图
sns.heatmap(cm, annot = True, cmap = 'GnBu')
plt.xlabel('Real Label')
plt.ylabel('Predict Label')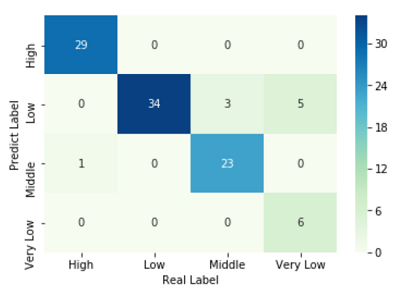
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17from sklearn import metrics
print('模型整体的预测准确率:', metrics.scorer.accuracy_score(y_test, pred))
print('分类模型的评估报告:\n', metrics.classification_report(y_test, pred))
**out:**
模型整体的预测准确率: 0.9108910891089109
分类模型的评估报告:
precision recall f1-score support
High 1.00 0.97 0.98 30
Low 0.81 1.00 0.89 34
Middle 0.96 0.88 0.92 26
Very Low 1.00 0.55 0.71 11
micro avg 0.91 0.91 0.91 101
macro avg 0.94 0.85 0.88 101
weighted avg 0.93 0.91 0.91 101
评估报告中,第一列precision表示模型的预测精准率,计算公式为“正确预测某类别的样本量/该类别预测样本个数”,第二列recall表示预测覆盖率,计算公式为“正确预测某类别的样本量/该类别的实际样本个数”,第三列f1-score是对precision和recall的加权结果,第四列为类别实际的样本个数。
2 预测问题的解决
读取数据集:1
2ccpp = pd.read_excel(r'C:\Users\Q\Desktop\CCPP.xlsx')
ccpp.head()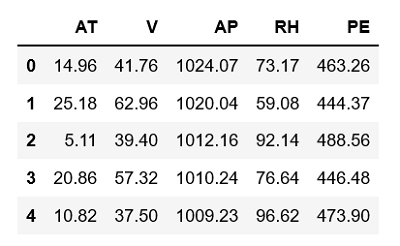
前4列为自变量,最后一列为连续型的因变量。
由于4个自变量的量纲不一致,要做标准化处理。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22from sklearn.preprocessing import minmax_scale
predictors = ccpp.columns[:-1]
#对自变量数据做标准化处理
X = minmax_scale(ccpp[predictors])
X_train, X_test, y_train, y_test = train_test_split(X, ccpp.PE,
test_size = 0.25,
random_state = 1234)
#设置待测试的不同k值
K = np.arange(1, int(np.ceil(np.log2(ccpp.shape[0]))))
#构建空列表存储MSE
mse = []
for k in K:
cv_result = cross_val_score(neighbors.KNeighborsRegressor
(n_neighbors = k, weights = 'distance'),
X_train, y_train, cv = 10,
scoring = 'neg_mean_squared_error')
mse.append((-1 * cv_result).mean())
arg_min = np.array(mse).argmin()
plt.scatter(K, mse)
plt.plot(K, mse)
plt.text(K[arg_min], mse[arg_min] + 0.5, 'the best k is %s' %int(K[arg_min]))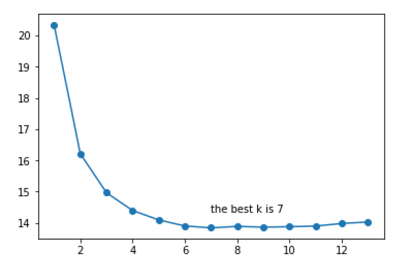
这里需要注意的是,衡量模型好坏的指标不再是准确率,而是MSE(均方误差)。
经过10重交叉验证,得到最佳的近邻个数为7,接下来利用这个最佳K值对训练集进行建模:1
2
3
4
5
6
7
8knn_reg = neighbors.KNeighborsRegressor(n_neighbors = 7, weights = 'distance')
knn_reg.fit(X_train,y_train)
pred = knn_reg.predict(X_test)
#计算MSE值
metrics.mean_squared_error(y_test, pred)
**out:**
12.814094947334912
对连续型因变量的预测问题来说,通常使用MSE或RMSE(均方误差根)评估模型好坏,该值越小,说明预测值与真实值越接近,模型拟合越好。这里可以对比一下测试集中的真实数据和预测数据,看看两者之间的差异:1
2pd.DataFrame({'Real': y_test, 'Predict': pred},
columns = ['Real', 'Predict']).head()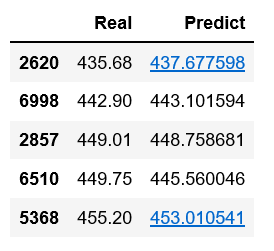
可以看到,KNN模型在测试集上的预测值和实际值非常接近,可以认为模型的拟合效果很理想。
3 决策树模型的对比
KNN算法和决策树非常类似,在建模时都对数据没有什么特殊要求,所以这里对比一下两个模型在CCPP数据集上的表现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28from sklearn.model_selection import GridSearchCV
from sklearn import tree
max_depth = [19, 21, 23, 25, 27]
min_samples_split = [2, 4, 6, 8]
min_samples_leaf = [2, 4, 8, 10, 12]
parameters = {'max_depth':max_depth,
'min_samples_split':min_samples_split,
'min_samples_leaf':min_samples_leaf}
grid_dtreg = GridSearchCV(estimator=tree.DecisionTreeRegressor(),
param_grid=parameters, cv = 10)
grid_dtreg.fit(X_train, y_train)
grid_dtreg.best_params_
**out:**
{'max_depth': 19, 'min_samples_leaf': 10, 'min_samples_split': 2}
#利用网格搜索法得到的最佳参数组合构造回归决策树
CART_Reg = tree.DecisionTreeRegressor(max_depth = 19,
min_samples_leaf = 10,
min_samples_split = 2)
CART_Reg.fit(X_train,y_train)
predict = CART_Reg.predict(X_test)
#计算MSE值
metrics.mean_squared_error(y_test, predict)
**out:**
16.17598770280405
结果显示,利用预测回归树对CCPP数据集进行建模,在测试集上得到的MSE值要比KNN模型的MSE值12.81大,说明决策树模型在CCPP数据集上的拟合效果没有KNN模型理想。
- 本笔记基于刘顺祥的《从零开始学Python数据分析与挖掘》整理

