决策树与随机森林

2020-02-21

字数统计: 1.9k字 | 阅读时长: 8分

决策树属于经典的十大数据挖掘算法之一，是一种类似于流程图的树结构，可用于数值型因变量的预测和离散型因变量的分类。通常情况下。将决策树用于分类器会有很好的预测准确率。sklearn模块选择了一种较优的决策树算法，即CART算法，它既可以处理离散型的分类问题（分类决策树），也可以解决连续型的预测问题（回归决策树），分别对应的是子模块tree的DecisionTreeClassifier类和DecisionTreeRegressor类。

随机森林属于集成算法，即随机生成构成多棵决策树的数据，生成过程中采用的是Bootstrap算法。sklearn的子模块ensemble提供了产生随机森林的RandomForestClassifier类和RandomForestRegressor类。

1 分类问题的解决

利用决策树和随机森林对Titanic数据集进行拟合。
首先导入常用的程序库和读取数据集：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
import pandas as pd

Titanic = pd.read_csv(r'C:\Users\Q\Desktop\Titanic.csv')
Titanic.head()

接下来对数据集进行清洗:

#删除无意义的变量，并检查剩余变量是否有缺失值
Titanic.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], 
             axis = 1, inplace = True)
Titanic.isnull().sum(axis = 0)

**out:**
Survived      0
Pclass        0
Sex           0
Age         177
SibSp         0
Parch         0
Fare          0
Embarked      2
dtype: int64

变量Embarked有2个缺失值，使用众数法进行填充；变量Age的缺失个数比较多，按照性别对客户的缺失年龄分组填充：

#对Sex分组，用各组乘客的平均年龄填充各组中的缺失年龄
fillna_Titanic = []
for i in Titanic.Sex.unique():
    update = Titanic.loc[Titanic.Sex == i,].fillna(
        value = {'Age': Titanic.Age[Titanic.Sex == i].mean()}, inplace = False)
    fillna_Titanic.append(update)
Titanic = pd.concat(fillna_Titanic)
#使用Embarked变量的众数填充缺失值
Titanic.fillna(value = {'Embarked': Titanic.Embarked.mode()[0]}, 
               inplace = True)

变量Pclass、Sex和Embarked均为离散变量，在建模前需要对其进行哑变量处理：

#将数值型的Pclass转换为类别型，否则无法对其进行哑变量处理
Titanic.Pclass = Titanic.Pclass.astype('category')
#哑变量处理
dummy = pd.get_dummies(Titanic[['Sex', 'Embarked', 'Pclass']])
Titanic = pd.concat([Titanic, dummy], axis = 1)
Titanic.drop(['Sex', 'Embarked', 'Pclass'], inplace = True, axis = 1)
Titanic.head()

1.1 构建决策树模型

from sklearn.model_selection import train_test_split
predictors = Titanic.columns[1:]
X_train, X_test, y_train, y_test = train_test_split(Titanic[predictors], 
                                                    Titanic.Survived, 
                                                    test_size = 0.25, 
                                                    random_state = 1234)

为了防止构建的决策树产生过拟合，需要对决策树进行预剪枝，如限制树生长的最大深度、设置决策树的中间节点能够继续分支的最小样本量以及叶节点的最小样本量等。
为了得到比较理想的树，需要不断尝试不同组合的参数值。这里可以使用网格搜索法，调用model_selection下的GridSearchCV类：

from sklearn.model_selection import GridSearchCV
from sklearn import tree
# 预设各参数的不同选项值
max_depth = [2,3,4,5,6]
min_samples_split = [2,4,6,8]
min_samples_leaf = [2,4,8,10,12]
# 将各参数值以字典形式组织起来
parameters = {'max_depth':max_depth, 
              'min_samples_split':min_samples_split, 
              'min_samples_leaf':min_samples_leaf}
# 网格搜索法，测试不同的参数值
grid_dtcateg = GridSearchCV(estimator = tree.DecisionTreeClassifier(), 
                            param_grid = parameters, cv=10)
# 模型拟合
grid_dtcateg.fit(X_train, y_train)
# 返回最佳组合的参数值
grid_dtcateg.best_params_

**out:**
{'max_depth': 3, 'min_samples_leaf': 4, 'min_samples_split': 2}

经过10重交叉验证的网格搜索，得到各参数的最佳组合值。
接下来利用这个组合值构建分类决策树：

#构建分类决策树
CART_Class = tree.DecisionTreeClassifier(max_depth = 3, 
                                         min_samples_leaf = 4, 
                                         min_samples_split = 2)
#模型拟合
decision_tree = CART_Class.fit(X_train, y_train)
#模型预测
pred = CART_Class.predict(X_test)

from sklearn import metrics
print('模型在测试集的预测准确率：', metrics.accuracy_score(y_test, pred))
print('模型在训练集的预测准确率：', 
      metrics.accuracy_score(y_train, CART_Class.predict(X_train)))

**out:**
模型在测试集的预测准确率：0.8295964125560538
模型在训练集的预测准确率：0.8038922155688623

模型在测试集的预测准确率83%，总体来说，预测精度还是比较高的，但该准确率无法体现正例和负例额覆盖率。为了进一步验证模型在测试集上的预测效果，接下来绘制ROC曲线：

import matplotlib.pyplot as plt

y_score = CART_Class.predict_proba(X_test)[:, 1]
fpr, tpr, threshold = metrics.roc_curve(y_test, y_score)
roc_auc = metrics.auc(fpr, tpr)
plt.stackplot(fpr, tpr, color = 'steelblue', 
              alpha = 0.5, edgecolor = 'black')
plt.plot(fpr, tpr, color = 'black', lw = 1)
plt.plot([0, 1], [0, 1], color = 'red', linestyle = '--')
plt.text(0.5, 0.3, 'ROC curve (area = %0.2f)' % roc_auc)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')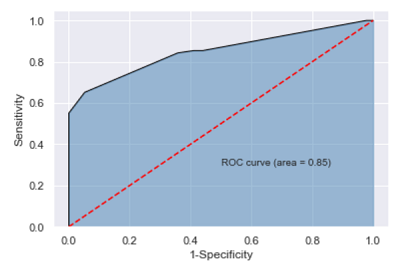

1.2 构建随机森林模型

# 导入第三方包
from sklearn import ensemble
# 构建随机森林
RF_class = ensemble.RandomForestClassifier(n_estimators=200, random_state=1234)
# 随机森林的拟合
RF_class.fit(X_train, y_train)
# 模型在测试集上的预测
RFclass_pred = RF_class.predict(X_test)
# 模型的准确率
print('模型在测试集的预测准确率：',
      metrics.accuracy_score(y_test, RFclass_pred))

**out:**
模型在测试集的预测准确率： 0.852017937219731

结果显示，采用随机森林对数据集进行分类，确实提高了测试数据集上的预测准确率，超过85%。
接下来对该模型产生的结果绘制ROC曲线：

# 计算绘图数据
y_score = RF_class.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
roc_auc = metrics.auc(fpr,tpr)
# 绘图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
plt.plot(fpr, tpr, color='black', lw = 1)
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
plt.show()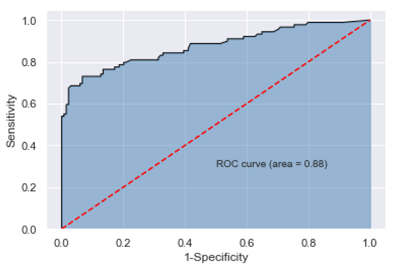

如图，AUC值为0.87，同样比单棵决策树的AUC值高。
最后，利用理想的随机森林算法挑选出影响因变量的重要因素：

# 变量的重要性程度值
importance = RF_class.feature_importances_
# 构建含序列用于绘图
Impt_Series = pd.Series(importance, index = X_train.columns)
# 对序列排序绘图
Impt_Series.sort_values(ascending = True).plot('barh')
plt.show()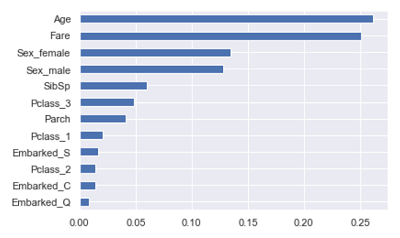

如图对自变量的重要性进行降序排序，最重要的三个变量分别是乘客的年龄、票价和是否为女性。

2 预测问题的解决

预测问题使用的是连续的数据值，首先读入数据：

1 2	nhanes = pd.read_excel(r'C:\Users\Q\Desktop\NHANES.xlsx') nhanes.head()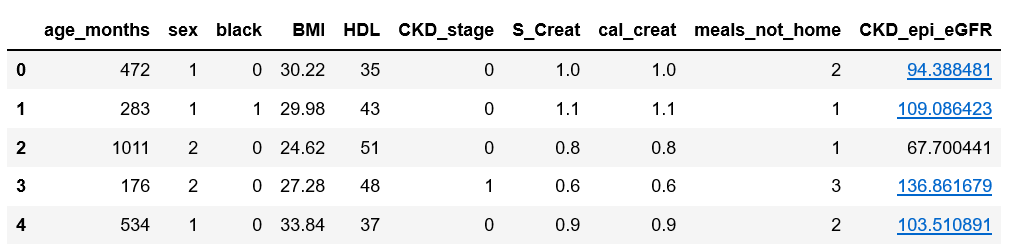

2.1 构建决策树模型

from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn import tree

predictors = nhanes.columns[:-1]
X_train, X_test, y_train, y_test = train_test_split(nhanes[predictors], 
                                                    nhanes.CKD_epi_eGFR, 
                                                    test_size = 0.25, 
                                                    random_state = 1234)
# 预设各参数的不同选项值
max_depth = [18, 19, 20, 21, 22]
min_samples_split = [2, 4, 6, 8]
min_samples_leaf = [2, 4, 8, 10, 12]
parameters = {'max_depth': max_depth, 
              'min_samples_split': min_samples_split, 
              'min_samples_leaf': min_samples_leaf}
# 网格搜索法，测试不同的参数值
grid_dtcateg = GridSearchCV(estimator=tree.DecisionTreeRegressor(), 
                            param_grid=parameters, cv =10)
# 模型拟合
grid_dtcateg.fit(X_train, y_train)
# 返回最佳组合的参数值
grid_dtcateg.best_params_

**out:**
{'max_depth': 18, 'min_samples_leaf': 2, 'min_samples_split': 2}

经过10重交叉验证的网格搜索，得到各参数的最佳组合值。
接下来利用这个组合值构建回归决策树：

from sklearn import metrics

CART_Reg = tree.DecisionTreeRegressor(max_depth = 18, 
                                      min_samples_leaf = 2, 
                                      min_samples_split = 2)
CART_Reg.fit(X_train, y_train)
pred = CART_Reg.predict(X_test)
metrics.mean_squared_error(y_test, pred)

**out:**
1.7855672399722669

由于因变量为连续型的数值，因此不能用分类模型中的准确率指标进行评估，而要用均方误差MSE或均方根误差RMSE，该指标越小，说明模型的拟合效果越好。

2.2 构建随机森林模型

from sklearn import ensemble

RF = ensemble.RandomForestRegressor(n_estimators = 200, random_state = 1234)
RF.fit(X_train, y_train)
RF_pred = RF.predict(X_test)
metrics.mean_squared_error(y_test, RF_pred)

**out:**
0.8943765841580971

结果显示，随机森林算法在测试集上的MSE为0.9，比单棵决策树的MSE小了一半，说明随机森林的拟合效果要比单棵回归树理想。
最后，基于随机森林计算的变量重要性绘制条形图：

import matplotlib.pyplot as plt

importance = pd.Series(RF.feature_importances_, index = X_train.columns)
importance.sort_values().plot('barh')
plt.show()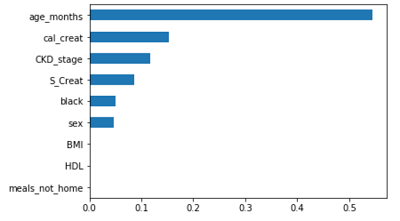

由图可以得出影响因变量的三个主要因素。

总结

决策树既可以解决分类问题，又可以解决预测问题。
而随机森林在解决单棵决策树的过拟合是一个非常不错的选择。

本笔记基于刘顺祥的《从零开始学Python数据分析与挖掘》整理