在实际应用中,当因变量为连续型时,可以用线性回归模型、岭回归模型和LASSO回归模型解决预测问题,当因变量为离散型时, 则需要Logistic回归模型来解决二分类的离散问题。
1 模型的构建
可以用sklearn子模块的linear_model中LogisticsRegression类。
首先导入常用的程序库和读取数据集:1
2
3
4
5
6import pandas as pd
import numpy as np
from sklearn import linear_model
sports = pd.read_csv(r'C:\Users\Q\Desktop\Run or Walk.csv')
sports.head()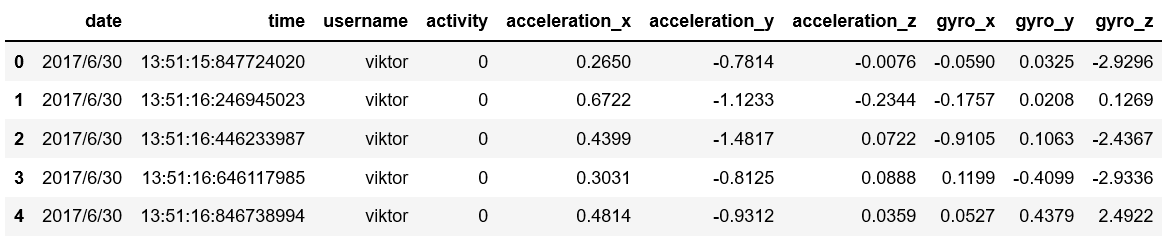
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19#提取自变量和因变量,并构造自变量矩阵
predictors = sports.columns[4:]
X = sports.ix[:, predictors]
y = sports.activity
#将数据集拆分为训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = 0.25,
random_state = 1234)
#用训练集建模
logistic = linear_model.LogisticRegression()
logistic.fit(X_train, y_train)
#返回模型的各个参数
print(logistic.intercept_, logistic.coef_)
**out:**
[4.35613952]
[[ 0.48533325 6.86221041 -2.44611637 -0.01344578 -0.1607943 0.13360777]]
得到截距项和参数后就可以得到模型的表达式了!
2 模型的预测
1 | pred = logistic.predict(X_test) |
以上结果表明,判断为步行状态的样本有12121个,跑步的样本有10026个。
单看这两个数据,无法判断模型预测得是否准确,接下来对模型预测效果做定量的评估。
3 模型的评估
分类模型的常用评估方法有混淆矩阵、ROC曲线和K-S曲线(该曲线太复杂了所以就不放上来了=.=)。
3.1 混淆矩阵
使用sklearn子模块的metrics中的confusion_matrix函数完成。1
2
3
4
5
6
7from sklearn import metrics
cm = metrics.confusion_matrix(y_test, pred, labels = [0, 1])
cm
**out:**
array([[9971, 1120],
[2150, 8906]], dtype=int64)
关于混淆矩阵可以看下图: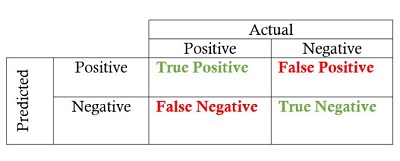
使用混淆矩阵评估模型的好坏,一般选用准确率Accuracy、正例覆盖率Sensitivity和负例覆盖率Specificity三种指标,其中:
- 准确率Accuracy:表示正确预测的正负例样本数与所有样本数量的比值。
- 正例覆盖率Sensitivity:表示正确预测的正例数在实际正例数中的比例。
- 负例覆盖率Specificity:表示正确预测的负例数在实际负例数中的比例。
计算过程如下:1
2
3
4
5
6
7
8
9
10
11accuracy = metrics.scorer.accuracy_score(y_test, pred)
sensitivity = metrics.scorer.recall_score(y_test, pred)
specificity = metrics.scorer.recall_score(y_test, pred, pos_label=0)
print('模型准确率为%.2f%%' %(accuracy * 100))
print('正例覆盖率为%.2f%%' %(sensitivity * 100))
print('负例覆盖率为%.2f%%' %(specificity * 100))
**out:**
模型准确率为85.24%
正例覆盖率为80.55%
负例覆盖率为89.90%
总体来说,模型的准确率还是蛮高的。
接下来还可以对该混淆矩阵作可视化展示,使用seaborn模块中的heatmap函数,即绘制热力图:1
2
3
4
5import seaborn as sns
import matplotlib.pyplot as plt
sns.heatmap(cm, annot = True, fmt = '.2e', cmap = 'GnBu')
plt.show()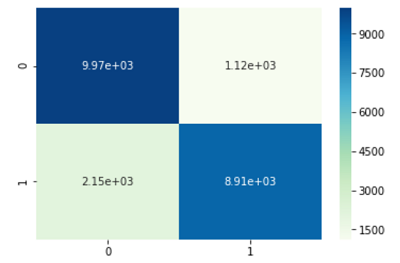
颜色越深的地方代表样本量越多,图中显示正确预测得正例和负例的样本数目非常大。
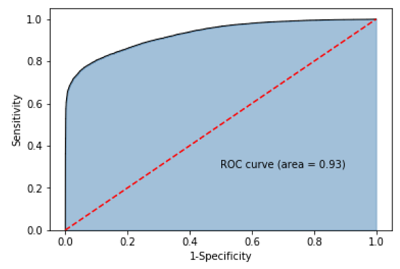
3.2 ROC曲线
1 | #y得分为模型预测正例的概率 |
4 另一种实现Logistic回归模型的方法
即:statsmodels1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45#----------------------------第一步:建模------------------------------#
import statsmodels.api as sm
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = 0.25,
random_state = 1234)
#为训练集和测试集的x矩阵添加常数列1
X_train2 = sm.add_constant(X_train)
X_test2 = sm.add_constant(X_test)
拟合Logistic模型
sm_logistic = sm.formula.Logit(y_train,X_train2).fit()
sm_logistic.params
**out:**
const 4.388537
acceleration_x 0.489617
acceleration_y 6.906590
acceleration_z -2.459638
gyro_x -0.014715
gyro_y -0.161164
gyro_z 0.134655
dtype: float64
#------------------------第二步:预测构建混淆矩阵------------------------#
sm_pred = sm_logistic.predict(X_test2)
#根据概率值,将观测进行分类,以0.5为阈值
sm_pred_y = np.where(sm_pred >= 0.5, 1, 0)
cm = metrics.confusion_matrix(y_test, sm_pred_y, labels = [0,1])
cm
**out:**
array([[9967, 1124],
[2149, 8907]], dtype=int64)
#--------------------------第三步:绘制ROC曲线--------------------------#
fpr, tpr, threshold = metrics.roc_curve(y_test, sm_pred)
roc_auc = metrics.auc(fpr, tpr)
plt.stackplot(fpr, tpr, color = 'steelblue',
alpha = 0.5, edgecolor = 'black')
plt.plot(fpr, tpr, color = 'black', lw = 1)
plt.plot([0,1], [0,1], clor = 'red', linestyle = '--')
plt.text(0.5, 0.3, 'ROC curve (area = %0.2f)' % roc_auc)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
plt.show()
图就不放上来了,以上代码有两点需要注意:
一是用Logit类,需要拟合模型的截距项,运用add_constant函数,增加常数为1的列;
二是对模型进行预测时,并不是返回具体的某个分类,而是样本被预测为正例的概率值。所以如果需要具体的样本分类,还需要对概率值进行切分,即大于等于0.5为正例,否则为负例。
- 本笔记基于刘顺祥的《从零开始学Python数据分析与挖掘》整理

