Processing math: 100%

岭回归与LASSO回归模型

字数统计: 1.5k字   |   阅读时长: 6分

线性回归模型在实际应用中，可能会出现自变量个数多于样本量或者自变量间存在多重共线性的情况，此时无法估计回归系数。而岭回归和LASSO回归则可以解决这类问题。

1 岭回归模型

线性回归模型的参数估计公式为β=[(X^’ X)]^(-1) X^’y，为解决自变量个数多于样本量或者自变量间存在多重共线性而导致偏回归系数无解的情况，岭回归模型对此进行修正，加入惩罚项系数λ，模型系数表达式为β=[(X^’ X + λI)]^(-1) X^’y，所以关键点是找到合理的λ值。λ值的确定有两种方法，可视化和交叉验证法。

1.1 可视化方法确定λ值

可以用sklearn子模块linear_model中的Ridge类实现模型系数的求解。
首先导入常用的程序库和读取数据集：

1
2
3
4
5
6
7
8
9
10
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge,RidgeCV

diabetes = pd.read_excel(r'C:\Users\Q\Desktop\diabetes.xlsx',sep = ' ')
diabetes.head()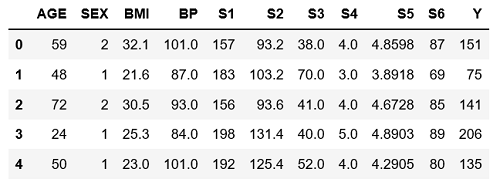


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#构造自变量
predictors = diabetes.columns[2:-1]
#将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(diabetes[predictors], 
                                                    diabetes['Y'], 
                                                    test_size = 0.2, 
                                                    random_state = 1234)
#构造不同的lambda值
Lambdas = np.logspace(-5, 2, 200)
#构造空列表用于存储模型的偏回归系数
ridge_cofficients = []
#迭代不同的lambda值
for Lambda in Lambdas:
    ridge = Ridge(alpha = Lambda, normalize=True)
    ridge.fit(X_train, y_train)
    ridge_cofficients.append(ridge.coef_)

#绘制alpha值与偏回归系数的关系
plt.plot(Lambdas, ridge_cofficients)
plt.xscale('log')
plt.xlabel('Log(Lambda)')
plt.ylabel('Cofficients')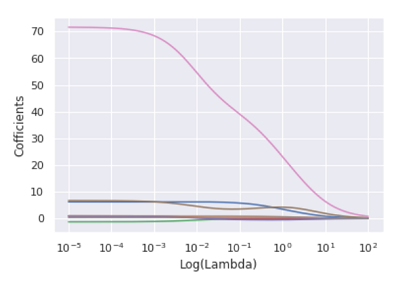


图中的每条折线代表了不同的变量，对于比较突出的喇叭形折线，一般代表该变量存在多重共线性。当λ值在0.01附近时，绝大多数变量的回归系数趋于稳定，故认为λ值可以选择在0.01附近。

1.2 交叉验证法确定λ值

可以用sklearn子模块linear_model中的RidgeCV类实现岭回归模型的k重交叉验证。

1
2
3
4
5
6
7
8
9
#设置交叉验证的参数，对于每个Lambda值，都执行10重交叉验证
ridge_cv = RidgeCV(alphas = Lambdas, normalize=True, 
                   scoring='neg_mean_squared_error', cv = 10)
ridge_cv.fit(X_train, y_train)
ridge_best_Lambda = ridge_cv.alpha_
ridge_best_Lambda

**out:**
0.013509935211980266

结果与可视化确定的λ值保持一致。

1.3 模型的预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#基于最佳的Lambda值建模
ridge = Ridge(alpha = ridge_best_Lambda, normalize=True)
ridge.fit(X_train, y_train)
#返回岭回归系数
pd.Series(index = ['Intercept'] + X_train.columns.tolist(),
         data = [ridge.intercept_] + ridge.coef_.tolist())

**out:**
Intercept   -324.753274
BMI            6.210754
BP             0.927874
S1            -0.503593
S2             0.223521
S3             0.045903
S4             4.252818
S5            52.075449
S6             0.383615
dtype: float64

基于上述结果就可得到岭回归模型的表达式啦！
接下来用该模型对测试集中的数据进行预测：

1
2
3
4
5
6
7
8
from sklearn.metrics import mean_squared_error

ridge_predict = ridge.predict(X_test)
RMSE = np.sqrt(mean_squared_error(y_test, ridge_predict))
RMSE

**out:**
53.12361694661972

使用均方根误差RMSE对模型的预测效果做定量的统计值，对于该统计量，值越小，说明模型对数据的拟合效果越好。

2 LASSO回归模型

与岭回归模型类似，LASSO回归同样属于缩减性估计，而且在回归系数的缩减过程中，可以将一些不重要的回归系数直接缩减为0，即达到变量筛选的功能（而岭回归不管怎么缩减，始终保留建模时的所有变量），原本在岭回归模型中的惩罚项由平方和改成了绝对值。同样，可用可视化和交叉验证法确定λ值。

2.1 可视化方法确定λ值

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.linear_model import Lasso,LassoCV

lasso_cofficients = []
for Lambda in Lambdas:
    lasso = Lasso(alpha = Lambda, normalize=True, max_iter=10000)
    lasso.fit(X_train, y_train)
    lasso_cofficients.append(lasso.coef_)
    
plt.plot(Lambdas, lasso_cofficients)
plt.xscale('log')
plt.xlabel('Lambda')
plt.ylabel('Cofficients')


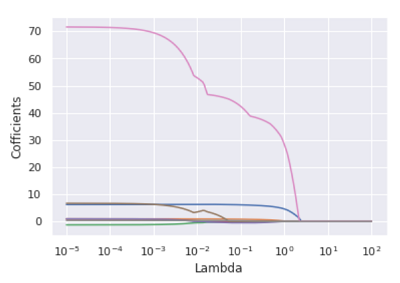
由图可知，当λ值落在0.05附近时，绝大多数变量的回归系数趋于稳定。

2.2 交叉验证法确定λ值

可以用sklearn子模块linear_model中的LassoCV类实现LASSO回归模型的k重交叉验证。

1
2
3
4
5
6
7
8
lasso_cv = LassoCV(alphas = Lambdas, normalize=True, 
                   cv = 10, max_iter=10000)
lasso_cv.fit(X_train, y_train)
lasso_best_alpha = lasso_cv.alpha_
lasso_best_alpha

**out:**
0.06294988990221888

最终得到合理的λ值为0.0629，与可视化方法得到的λ值范围基本保持一致。

2.3 模型的预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
lasso = Lasso(alpha = lasso_best_alpha, normalize=True, max_iter=10000)
lasso.fit(X_train, y_train)
pd.Series(index = ['Intercept'] + X_train.columns.tolist(),
         data = [lasso.intercept_] + lasso.coef_.tolist())

**out:**
Intercept   -278.560358
BMI            6.188602
BP             0.860826
S1            -0.127627
S2            -0.000000
S3            -0.488408
S4             0.000000
S5            44.487738
S6             0.324076
dtype: float64

系数中含有两个0，说明这两个变量对因变量没有显著意义，基于此可得LASSO回归模型的表达式。
接下来用该模型对测试集中的数据进行预测，计算出用于评估模型好坏的均方根误差RMSE：

1
2
3
4
5
6
lasso_predict = lasso.predict(X_test)
RMSE= np.sqrt(mean_squared_error(y_test, lasso_predict))
RMSE

**out:**
53.06143725822573

该RMSE比岭回归的RMSE值大约下降0.8，说明在降低模型复杂度的情况下（模型删除了两个变量），进一步提升了模型的拟合效果。
所以，绝大多数情况下，LASSO回归得到的系数比岭回归模型更加可靠和易于理解。

3 多元线性回归模型

用多元线性回归模型对比前面两种模型在同一数据集上的拟合效果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from statsmodels import api as sms
#为自变量X添加常数列1，用于拟合截距项
X_train2 = sms.add_constant(X_train)
X_test2 = sms.add_constant(X_test)

linear = sms.formula.OLS(y_train, X_train2).fit()
linear.params

**out:**
const   -406.699716
BMI        6.217649
BP         0.948245
S1        -1.264772
S2         0.901368
S3         0.962373
S4         6.694215
S5        71.614661
S6         0.376004
dtype: float64

需要注意的是，构建多元线性回归模型使用的是OLS类，该类在建模时不拟合截距项，为了得到模型的截距项，需要在训练集和测试集的自变量矩阵中添加常数列1。基于以上结果可以得到多元线性回归模型的表达式。
1
2
3
4
5
6
linear_predict = linear.predict(X_test2)
RMSE= np.sqrt(mean_squared_error(y_test, linear_predict))
RMSE

**out:**
53.42623939722987

结果显示，在对模型结果不做任何假设检验和拟合诊断的情况下，线性回归模型的拟合效果在三个模型中是最差的（RMSE值最大）。

  • 本笔记基于刘顺祥的《从零开始学Python数据分析与挖掘》整理
赏

谢谢你请我吃糖果

微信

扫一扫，分享到微信

微信分享二维码