线性回归预测模型

2020-02-15

字数统计: 2.4k字 | 阅读时长: 10分

线性回归模型属于一种有监督的学习算法，建模过程中必须同时具备自变量x和因变量y。

先导入常用的程序库：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
import numpy as np
import pandas as pd

1 一元线性回归模型

加载数据并画出拟合的散点图：

1 2	income = pd.read_csv(r'C:\Users\Q\Desktop\Salary_Data.csv') sns.lmplot(x = 'YearsExperience', y = 'Salary', data = income, ci = None)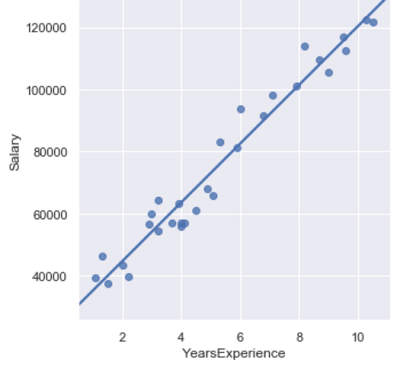

拟合线的求解

实现线性回归模型的参数求解，可以调用statsmodels子模块formula的ols函数。

import statsmodels.api as sm
fit = sm.formula.ols('Salary ~ YearsExperience',data = income).fit()
fit.params

**out:**
Intercept          25792.200199
YearsExperience     9449.962321
dtype: float64

将参数代入一元线性方程模型就可以啦！

2 多元线性回归模型

系数求解

1 2	Profit = pd.read_excel(r'C:\Users\Q\Desktop\Predict to Profit.xlsx') Profit.head()

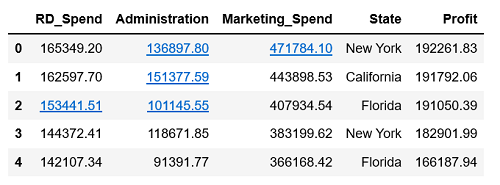
由于变量State为非数值型的离散变量，建模时需将其设置为哑变量处理，将其放在C()中，作为分类（Category）变量处理。

from sklearn import model_selection
train, test = model_selection.train_test_split(Profit, test_size = 0.2, 
						random_state = 1234)
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend 
			+ C(State)', data = train).fit()
print('模型的偏回归系数分别为：\n', model.params)

**out:**
模型的偏回归系数分别为：
 Intercept               58581.516503
C(State)[T.Florida]       927.394424
C(State)[T.New York]     -513.468310
RD_Spend                    0.803487
Administration             -0.057792
Marketing_Spend             0.013779
dtype: float64

产生的两个值State[Florida]和State[New York]，另一个State[California]成为对照组。如果想指定某个值作为对照组，可以通过pandas模块中的get_dummies函数生成哑变量，然后将所需的对照组对应的哑变量删除。

#生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
#将哑变量和原始数据集水平合并
Profit_New = pd.concat([Profit, dummies], axis = 1)
#删除State变量和New York变量（因为State变量已分解为哑变量，New York变量作为参照组）
Profit_New.drop(labels = ['State', 'New York'], axis = 1, inplace = True)
#拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, 
						random_state = 1234)
#建模
model2 = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend 
			+ Florida + California', data = train).fit()
print('模型的偏回归系数分别为：\n', model2.params)

**out:**
模型的偏回归系数分别为：
 Intercept          58068.048193
RD_Spend               0.803487
Administration        -0.057792
Marketing_Spend        0.013779
Florida             1440.862734
California           513.468310
dtype: float64

3 回归模型的假设检验

3.1 模型的显著性检验——F检验

获得模型的F统计量值和F分布的理论值：

print(model2.fvalue)
#计算F分布的理论值
from scipy import stats
p = model2.df_model
n = train.shape[0]
F_Theroy = stats.f.ppf(q = 0.95, dfn = p, dfd = n -p -1)
print('F分布的理论值为：', F_Theroy)

**out:**
174.63721715703542
F分布的理论值为： 2.502635007415366

由此可知，计算出来的F统计量的值174.64远远大于理论值2.5，所以拒绝原假设，即回归模型是显著的。

3.2 回归系数的显著性检验——t检验

接下来对模型的回归系数作显著性检验，看每个自变量对因变量是否都有显著意义。

1	model2.summary()

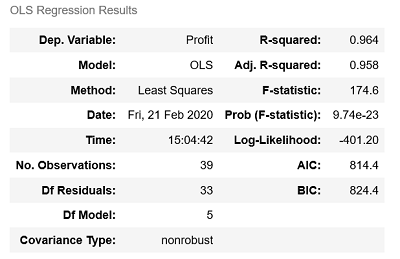
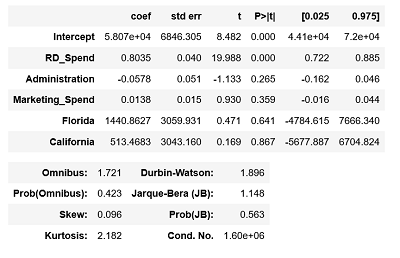
由结果可知，只有截距项Intercept和研发成本RD_Spend对应的p值小于0.05，说明其余变量没有通过系数显著性检验，即这些变量在模型中不是影响利润的重要因素。

4 回归模型的诊断

线性回归模型要满足的几个假设前提：
-误差项服从正态分布
-无多重共线性
-线性相关性
-误差项的独立性
-方差齐性

4.1 正态性检验

1）直方图法

import scipy.stats as stats
sns.distplot(a = Profit_New.Profit, bins = 10, fit = stats.norm, norm_hist = True,
             hist_kws = {'color':'steelblue', 'edgecolor':'black'}, 
             kde_kws = {'color':'black', 'linestyle':'--', 'label':'核密度曲线'}, 
             fit_kws = {'color':'red', 'linestyle':':', 'label':'正态密度曲线'})
plt.legend()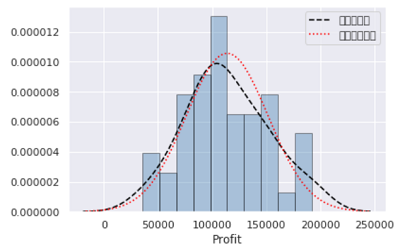

核密度曲线和正态密度曲线的趋势比较吻合，直观上可以认为利润变量服从正态分布。

2）PP图和QQ图

pp_qq_plot = sm.ProbPlot(Profit_New.Profit)
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')

pp_qq_plot.qqplot(line = 'q')
plt.title('Q-Q图')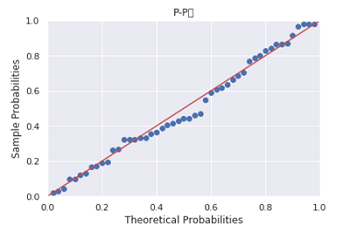

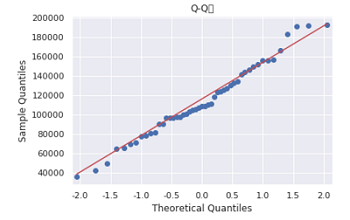
PP图和QQ图的点都落在直线附近，没有较大的分离，可以认为利润变量服从正态分布。

4.2 多重共线性检验

多重共线性的检验可以用方差膨胀因子VIF来鉴定，如果VIF大于10，则说明变量间存在多重共线性；如果VIF大于100，则说明存在严重的多重共线性。

from statsmodels.stats.outliers_influence import variance_inflation_factor
#自变量X（包含RD_Spend，Marketing_Spend和常数列1）
X = sm.add_constant(Profit_New.ix[:, ['RD_Spend', 'Marketing_Spend']])
vif = pd.DataFrame()
vif['feature'] = X.columns
vif['VIF Factor'] = [variance_inflation_factor(X.values, i) 
	              for i in range(X.shape[1])]
vif

结果显示两变量的方差膨胀因子均小于10，说明构建模型的数据不存在多重共线性。

4.3 线性相关性检验

相关系数的计算可以直接用数据框的corrwith方法：

#计算每个自变量与因变量之间的相关系数
Profit_New.drop('Profit', axis = 1).corrwith(Profit_New.Profit)

**out:**
RD_Spend           0.978437
Administration     0.205841
Marketing_Spend    0.739307
California        -0.083258
Florida            0.088008
dtype: float64

结果显示自变量中只有RD_Spend和Marketing_Spend与因变量有较高的相关

还可以用seaborn模块中的pairplot函数绘制散点图：

1	sns.pairplot(Profit_New.ix[:，['RD_Spend','Administration','Marketing_Spend','Profit']])

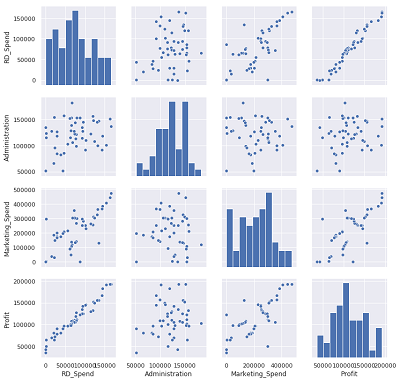
此时只保留RD_Spend和Marketing_Spend两个自变量，重新对模型进行修正：

model3 = sm.formula.ols("Profit ~ RD_Spend + Marketing_Spend", data = train).fit()
model3.params

**out:**
Intercept          51902.112471
RD_Spend               0.785116
Marketing_Spend        0.019402
dtype: float64

4.4 异常值检验

包括：帽子矩阵、DFFITS准则、学生化残差或Cook距离三种方法。

#异常值检验
outliers = model3.get_influence()
#帽子矩阵
leverage = outliers.hat_matrix_diag
#dffits值
dffits = outliers.dffits[0]
#学生化残差
resid_stu = outliers.resid_studentized_external
#cook距离
cook = outliers.cooks_distance[0]
#合并各种异常值检验的统计量值
contat1 = pd.concat([pd.Series(leverage, name = 'leverage'), 
		    pd.Series(dffits, name = 'dffits'), 
		    pd.Series(resid_stu, name = 'resid_stu'), 
		    pd.Series(cook, name = 'cook')], axis = 1)
train.index = range(train.shape[0])
profit_outliers = pd.concat([train, contat1],axis = 1)
profit_outliers.head()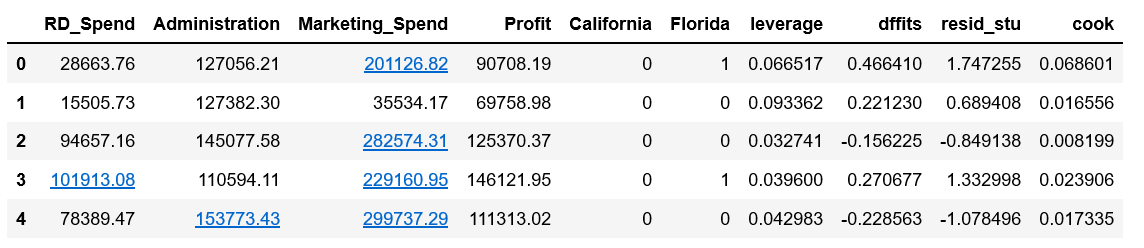

这里使用标准化残差将异常点查询出来，当标准化残差大于2时，即认为对应的数据点为异常值。

outliers_ratio = sum(np.where((np.abs(profit_outliers.resid_stu) > 2), 1, 0)) 
		/ profit_outliers.shape[0]
outliers_ratio

**out:**
0.02564102564102564

计算异常值比例为2.5%。当异常值比例不高（如小于等于5%），可以将异常值删除；如果比例较高，删除会丢失信息，可以选择衍生哑变量，即对于异常点，设置哑变量的值为1，否则为0.

#将resid_stu小于等于2的值删掉
none_outliers = profit_outliers.ix[np.abs(profit_outliers.resid_stu) <= 2,]
model4 = sm.formula.ols('Profit ~ RD_Spend + Marketing_Spend', 
			data = none_outliers).fit()
model4.params

**out:**
Intercept          51827.416821
RD_Spend               0.797038
Marketing_Spend        0.017740
dtype: float64

4.5 独立性检验

使用Durbin-Watson统计量来检验，如果DW值在2左右，表明残差之间是不相关的，如果与2偏离较远，则不满足残差的独立性检验。
可以用model4.summary()得出DW值。

4.6方差齐性检验

方差齐性要求模型残差项的方差不随自变量的变动而呈现某种趋势，否则，残差的趋势就可以被自变量刻画。
1）图形法

ax1 = plt.subplot2grid(shape = (2, 1), loc = (0, 0))
ax1.scatter(none_outliers.RD_Spend, 
	    (model4.resid - model4.resid.mean()) / model4.resid.std())
ax1.hlines(y = 0, xmin = none_outliers.RD_Spend.min(),
           xmax = none_outliers.RD_Spend.max(), color = 'red', linestyle = '--')
ax1.set_xlabel('RD_Spend')
ax1.set_ylabel('Std_Residual')

ax2 = plt.subplot2grid(shape = (2, 1), loc = (1, 0))
ax2.scatter(none_outliers.Marketing_Spend, 
	    (model4.resid - model4.resid.mean()) / model.resid.std())
ax2.hlines(y = 0, xmin = none_outliers.Marketing_Spend.min(),
           xmax = none_outliers.Marketing_Spend.max(), 
	   color = 'red', linestyle = '--')
ax2.set_xlabel('Marketing_Spend')
ax2.set_ylabel('Std_Residual')

plt.subplots_adjust(hspace = 0.6, wspace = 0.3)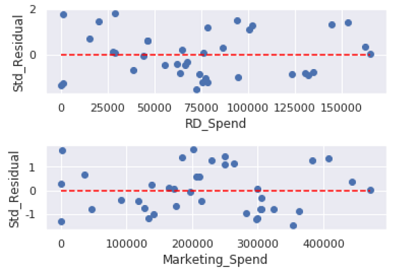

如图，所有的散点几乎均匀地分布在参考线y=0附近，说明模型的残差项满足方差齐性。

2）BP检验

sm.stats.diagnostic.het_breushpagan(model4.resid, exog_het = model4.model.exog)

**out:**
(1.467510366830809,
 0.48010272699006995,
 0.7029751237162342,
 0.5019659740962923)

第一个值为拉格朗日乘子LM统计量，第二个为其对应的概率值，大于0.05，说明接受残差方差为常数的原假设；第三个为F统计量，用于检验残差方差平方项与自变量之间是否独立，独立则说明残差方差齐性，第四个为F值的概率值。

5 回归模型的预测

经过前面的模型构造、假设检验和模型诊断，最终确定为model4，接下来对其进行预测：

pred4 = model4.predict(exog = test.ix[:, ['RD_Spend','Marketing_Spend']])
plt.scatter(x = test.Profit, y = pred4)
plt.plot([test.Profit.min(), test.Profit.max()], 
	 [test.Profit.min(), test.Profit.max()], 
	 color = 'red', linestyle = '--')
plt.xlabel('Real')
plt.ylabel('Prediction')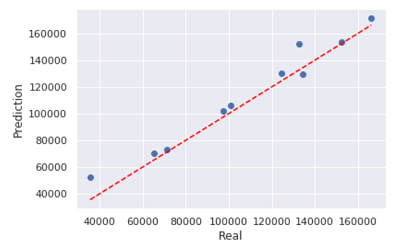

该散点图衡量了实际值和预测值之间的距离差异，由图可知，大部分的散点都落在对角线附近，说明模型的预测效果不错。

6 线性回归的其他方法

可以调用sklearn子模块linear_model的LinearRegression类，因为数据集中含有离散型变量State，所以不用该方法。接下来我去除这个变量，重新用LinearRegression拟合数据：

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

Profit = pd.read_excel(r'C:\Users\Q\Desktop\Predict to Profit.xlsx')
#选择前三个自变量
predictors = Profit.columns[0:3]
X = Profit.ix[:, predictors]
y = Profit.Profit
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size = 0.2, 
                                                    random_state = 1234)
#构建模型
regr = LinearRegression()
regr.fit(X_train, y_train)
print(regr.intercept_, regr.coef_)

**out:**
58468.79730227189 [ 0.8006243  -0.0555988   0.01469367]

可以和前面ols函数得出的结果对比一下，发现没差多少。

#模型预测
pred = regr.predict(X_test)
print('对比预测值和实际值的差异：\n', 
      pd.DataFrame({'Prediction': pred, 'Real': y_test}))
#返回返回预测性能得分
print('预测性能得分：%.2f' % regr.score(X_test, y_test))

**out:**
对比预测值和实际值的差异：
        Prediction       Real
8   151288.217174  152211.77
48   56025.918817   35673.41
14  149563.538650  132602.65
42   74222.952664   71498.49
29  104059.996681  101004.64
44   68034.140826   65200.33
4   172542.473581  166187.94
31  100222.275500   97483.56
13  128299.353217  134307.35
18  129910.819598  124266.90

预测性能得分：0.95

预测性能得分不超过1，但是可能为负值（预测效果太差），预测性能得分越大，预测性能越好。

本笔记基于刘顺祥的《从零开始学Python数据分析与挖掘》整理